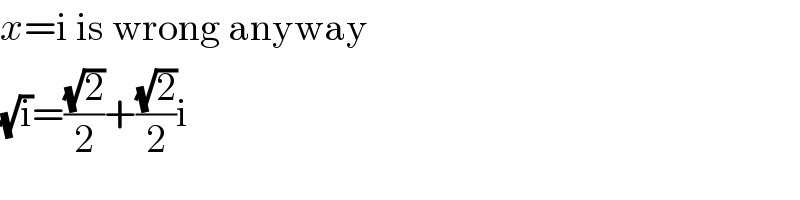Question and Answers Forum
Question Number 67903 by rajesh4661kumar@gmail.com last updated on 02/Sep/19

Answered by $@ty@m123 last updated on 02/Sep/19
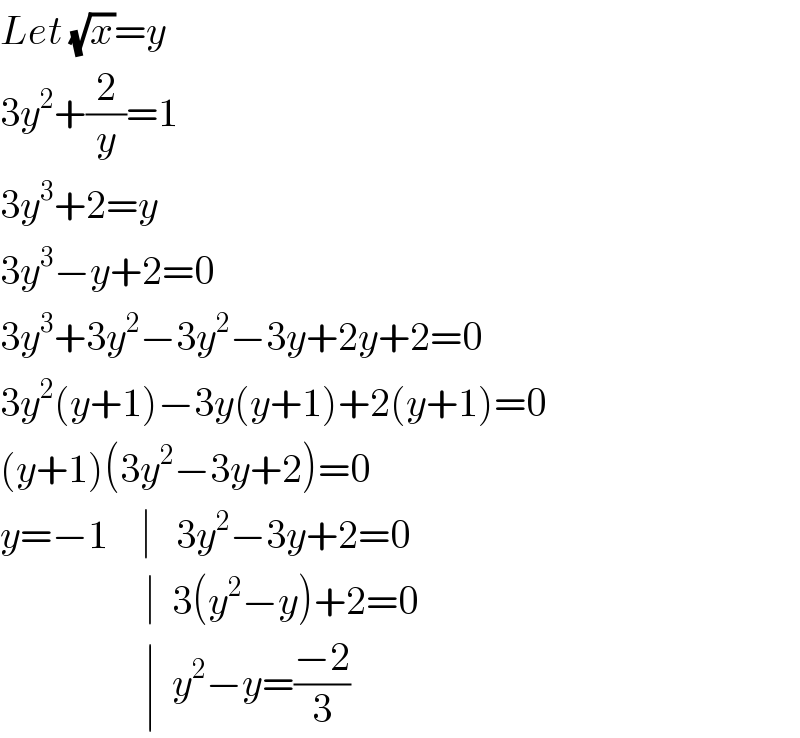
Commented by MJS last updated on 02/Sep/19
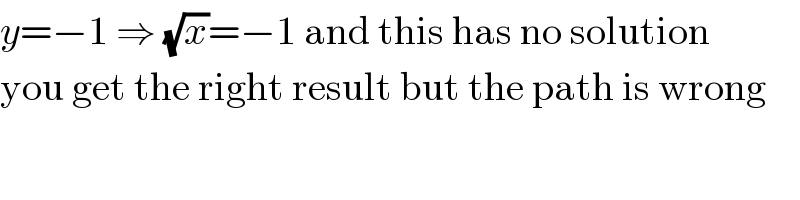
Commented by Prithwish sen last updated on 02/Sep/19
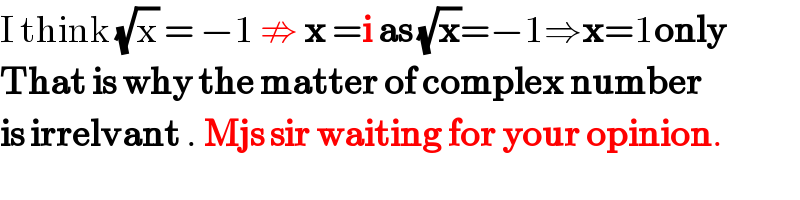
Commented by MJS last updated on 02/Sep/19

Commented by Prithwish sen last updated on 02/Sep/19
Answered by MJS last updated on 02/Sep/19

Commented by MJS last updated on 02/Sep/19