
Question and Answers Forum
Question Number 68960 by ajfour last updated on 17/Sep/19

Commented by TawaTawa last updated on 17/Sep/19

Commented by ajfour last updated on 17/Sep/19
![a=b=c=d=e=−1 λ^2 −λ−1=0 ⇒ λ=((1±(√5))/2) A=−λ^2 −λ−1=−(2+λ) =−(((5±(√5))/2)) Q_1 =q^2 −q−1 , Q_2 =−q^2 −q−1 L_1 =2λq++b(λ+q)+2d =2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =±(√5)q−(((5±(√5))/2)) L_2 =2aλq+c(λ+q)+2e =−2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =−(2±(√5))q−(((5±(√5))/2)) Now AQ_1 ^2 −L_1 L_2 Q_1 +L_1 ^2 Q_2 =0 −(((5±(√5))/2))(q^2 −q−1)^2 −[±(√5)q−(((5±(√5))/2))][−(2±(√5))q−(((5±(√5))/2))] ×(q^2 −q−1) +[±(√5)q−(((5±(√5))/2))]^2 (−q^2 −q−1)=0 ⇒ −2(5±(√5))(q^2 −q−1)^2 +[±2(√5)q−(5±(√5))][2(2±(√5))q+(5±(√5)] ×(q^2 −q−1) −[±2(√5)q−(5±(√5))]^2 (q^2 +q+1)=0 ⇒ let 5±(√5)=n ⇒ −2n(q^2 −q−1)^2 +[−10q+2nq−n] ×[−6q+2nq+n](q^2 −q−1) −[−10q+2nq−n]^2 (q^2 +q+1)=0 ⇒ −2n(q^2 −q−1)^2 + [(2n−10)(2n−6)q^2 −4nq−n^2 ] ×(q^2 −q−1)+ −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1) = 0 ⇒ −2n(q^4 −2q^3 −q^2 +2q+1)+ +{4(n−5)(n−3)q^4 −4q^3 [(n−5)(n−3)+n] −q^2 [4(n−5)(n−3)+n^2 −4n] +q(n^2 +4n)+n^2 } −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1)=0 ⇒ q^4 {−2n+4n^2 −32n+60 −4n^2 +40n−100} +q^3 {4n−4n^2 +28n−60 −4n^2 +40n−100 +4n^2 −20n} +q^2 {2n−5n^2 +36n−60 −4n^2 +40n−100 +4n^2 −20n−n^2 } +q{−4n+n^2 +4n 4n^2 −20n−n^2 } (−2n+n^2 −n^2 )=0 Reducing (6n−40)q^4 −(4n^2 −52n+160)q^3 −(6n^2 −58n+160)q^2 +4(n^2 −5n)q−2n=0 Again dividing by 2 (3n−20)q^4 −(2n^2 −26n+80)q^3 −(3n^2 −29n+80)q^2 +(2n^2 −10n)q−n=0 to remind again n=5±(√5) taking n_1 =5+(√5) n^2 (−2q^3 −3q^2 +2q)+ n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 since n=5±(√5) (n−5)^2 =5 n^2 −10n+20=0 n^2 =10n−20 So, i can write n(−20q^3 −30q^2 +20q) −20(−2q^3 −3q^2 +2q) n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) +(−20q^4 −40q^3 −20q^2 −40q)=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) −20(q^4 +2q^3 +q^2 +2q)=0 ________________________ (3n−20)(q^4 +2q^3 +q^2 +2q) −n(4q^2 −4q+1) = 0 _______________________ 3n−20 = −5±3(√5) = N 6n−40=−10±6(√5) −n−20 = −25∓(√5) = −((N+80)/3) 10n−40 = 10±10(√5) = 10(((N+8)/3)) ⇒ q^4 +2q^3 −(((N+80)/(3N)))q^2 +(((10N+80)/(3N)))q−(((N+20)/(3N)))=0](Q68968.png)
Commented by TawaTawa last updated on 17/Sep/19
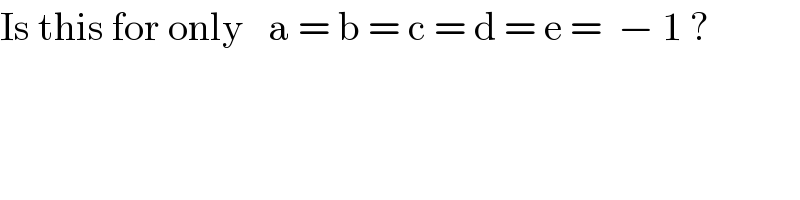
| ||
Question and Answers Forum | ||
Question Number 68960 by ajfour last updated on 17/Sep/19 | ||
 | ||
Commented by TawaTawa last updated on 17/Sep/19 | ||
 | ||
Commented by ajfour last updated on 17/Sep/19 | ||
![a=b=c=d=e=−1 λ^2 −λ−1=0 ⇒ λ=((1±(√5))/2) A=−λ^2 −λ−1=−(2+λ) =−(((5±(√5))/2)) Q_1 =q^2 −q−1 , Q_2 =−q^2 −q−1 L_1 =2λq++b(λ+q)+2d =2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =±(√5)q−(((5±(√5))/2)) L_2 =2aλq+c(λ+q)+2e =−2(((1±(√5))/2))q−((1±(√5))/2)−q−2 =−(2±(√5))q−(((5±(√5))/2)) Now AQ_1 ^2 −L_1 L_2 Q_1 +L_1 ^2 Q_2 =0 −(((5±(√5))/2))(q^2 −q−1)^2 −[±(√5)q−(((5±(√5))/2))][−(2±(√5))q−(((5±(√5))/2))] ×(q^2 −q−1) +[±(√5)q−(((5±(√5))/2))]^2 (−q^2 −q−1)=0 ⇒ −2(5±(√5))(q^2 −q−1)^2 +[±2(√5)q−(5±(√5))][2(2±(√5))q+(5±(√5)] ×(q^2 −q−1) −[±2(√5)q−(5±(√5))]^2 (q^2 +q+1)=0 ⇒ let 5±(√5)=n ⇒ −2n(q^2 −q−1)^2 +[−10q+2nq−n] ×[−6q+2nq+n](q^2 −q−1) −[−10q+2nq−n]^2 (q^2 +q+1)=0 ⇒ −2n(q^2 −q−1)^2 + [(2n−10)(2n−6)q^2 −4nq−n^2 ] ×(q^2 −q−1)+ −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1) = 0 ⇒ −2n(q^4 −2q^3 −q^2 +2q+1)+ +{4(n−5)(n−3)q^4 −4q^3 [(n−5)(n−3)+n] −q^2 [4(n−5)(n−3)+n^2 −4n] +q(n^2 +4n)+n^2 } −[(2n−10)^2 q^2 −2n(2n−10)q+n^2 ] ×(q^2 +q+1)=0 ⇒ q^4 {−2n+4n^2 −32n+60 −4n^2 +40n−100} +q^3 {4n−4n^2 +28n−60 −4n^2 +40n−100 +4n^2 −20n} +q^2 {2n−5n^2 +36n−60 −4n^2 +40n−100 +4n^2 −20n−n^2 } +q{−4n+n^2 +4n 4n^2 −20n−n^2 } (−2n+n^2 −n^2 )=0 Reducing (6n−40)q^4 −(4n^2 −52n+160)q^3 −(6n^2 −58n+160)q^2 +4(n^2 −5n)q−2n=0 Again dividing by 2 (3n−20)q^4 −(2n^2 −26n+80)q^3 −(3n^2 −29n+80)q^2 +(2n^2 −10n)q−n=0 to remind again n=5±(√5) taking n_1 =5+(√5) n^2 (−2q^3 −3q^2 +2q)+ n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 since n=5±(√5) (n−5)^2 =5 n^2 −10n+20=0 n^2 =10n−20 So, i can write n(−20q^3 −30q^2 +20q) −20(−2q^3 −3q^2 +2q) n(3q^4 +26q^3 +29q^2 −10q−1)+ 1(−20q^4 −80q^3 −80q^2 )=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) +(−20q^4 −40q^3 −20q^2 −40q)=0 ⇒ n(3q^4 +6q^3 −q^2 +10q−1) −20(q^4 +2q^3 +q^2 +2q)=0 ________________________ (3n−20)(q^4 +2q^3 +q^2 +2q) −n(4q^2 −4q+1) = 0 _______________________ 3n−20 = −5±3(√5) = N 6n−40=−10±6(√5) −n−20 = −25∓(√5) = −((N+80)/3) 10n−40 = 10±10(√5) = 10(((N+8)/3)) ⇒ q^4 +2q^3 −(((N+80)/(3N)))q^2 +(((10N+80)/(3N)))q−(((N+20)/(3N)))=0](Q68968.png) | ||
Commented by TawaTawa last updated on 17/Sep/19 | ||
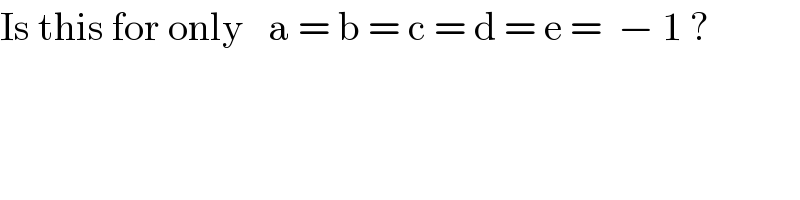 | ||