
Question and Answers Forum
Question Number 71538 by mr W last updated on 16/Oct/19

Commented by mr W last updated on 16/Oct/19

Answered by ajfour last updated on 17/Oct/19
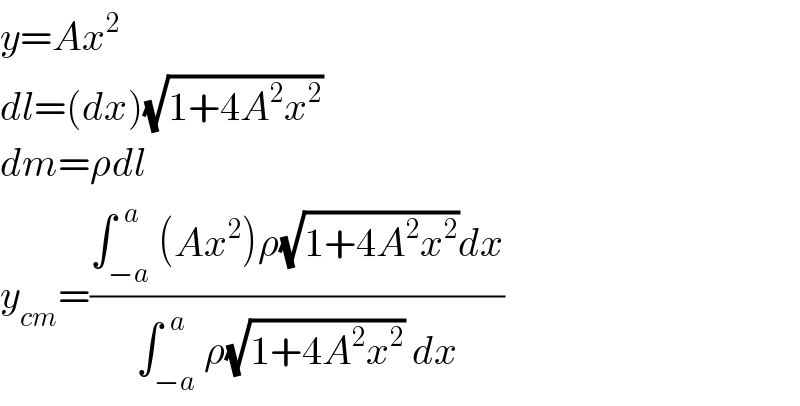
Answered by mr W last updated on 17/Oct/19
![y=((4Hx^2 )/L^2 )=Ax^2 A=((4H)/L^2 ) let λ=AL=((4H)/L) h_S =((∫_0 ^(L/2) Ax^2 (√(1+(2Ax)^2 ))dx)/(∫_0 ^(L/2) (√(1+(2Ax)^2 ))dx)) h_S =(1/(4A))×((∫_0 ^(L/2) (2Ax)^2 (√(1+(2Ax)^2 ))d(2Ax))/(∫_0 ^(L/2) (√(1+(2Ax)^2 ))d(2Ax))) h_S =(1/(4A))×((∫_0 ^(AL) t^2 (√(1+t^2 ))dt)/(∫_0 ^(AL) (√(1+t^2 ))dt)) ∫_0 ^λ (√(1+t^2 ))dt=[((ln ((√(1+t^2 ))+t)+t(√(1+t^2 )))/2)]_0 ^λ =((ln ((√(1+λ^2 ))+λ)+λ(√(1+λ^2 )))/2) ∫_0 ^λ t^2 (√(1+t^2 ))dt=[((t(2t^2 +1)(√(1+t^2 ))−ln ((√(1+t^2 ))+t))/8)]_0 ^λ =((λ(2λ^2 +1)(√(1+λ^2 ))−ln ((√(1+λ^2 ))+λ))/8) h_S =(L/(4λ))×((∫_0 ^λ t^2 (√(1+t^2 ))dt)/(∫_0 ^λ (√(1+t^2 ))dt)) =(L/(4λ))×((λ(2λ^2 +1)(√(1+λ^2 ))−ln ((√(1+λ^2 ))+λ))/8)×(2/(ln ((√(1+λ^2 ))+λ)+λ(√(1+λ^2 )))) =(L/(16))×(((2λ^2 +1)(√(1+λ^2 ))−((ln ((√(1+λ^2 ))+λ))/λ))/((√(1+λ^2 ))+((ln ((√(1+λ^2 ))+λ))/λ))) ⇒(h_S /H)=(1/(4λ))[((2(1+λ^2 )^(3/2) )/((√(1+λ^2 ))+((ln ((√(1+λ^2 ))+λ))/λ)))−1]](Q71594.png)
| ||
Question and Answers Forum | ||
Question Number 71538 by mr W last updated on 16/Oct/19 | ||
 | ||
Commented by mr W last updated on 16/Oct/19 | ||
 | ||
Answered by ajfour last updated on 17/Oct/19 | ||
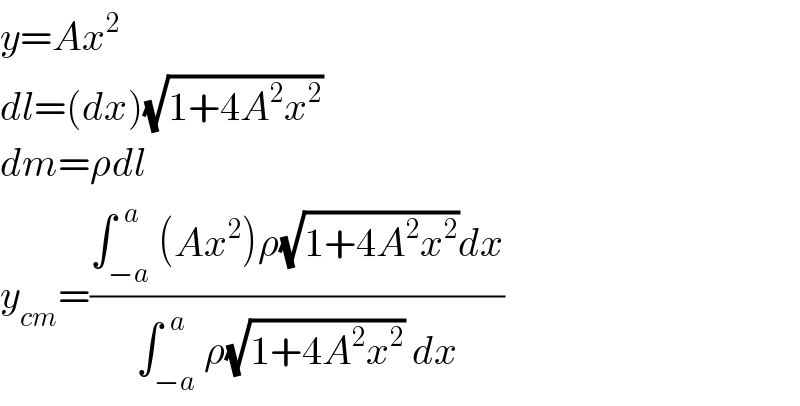 | ||
| ||
Answered by mr W last updated on 17/Oct/19 | ||
![y=((4Hx^2 )/L^2 )=Ax^2 A=((4H)/L^2 ) let λ=AL=((4H)/L) h_S =((∫_0 ^(L/2) Ax^2 (√(1+(2Ax)^2 ))dx)/(∫_0 ^(L/2) (√(1+(2Ax)^2 ))dx)) h_S =(1/(4A))×((∫_0 ^(L/2) (2Ax)^2 (√(1+(2Ax)^2 ))d(2Ax))/(∫_0 ^(L/2) (√(1+(2Ax)^2 ))d(2Ax))) h_S =(1/(4A))×((∫_0 ^(AL) t^2 (√(1+t^2 ))dt)/(∫_0 ^(AL) (√(1+t^2 ))dt)) ∫_0 ^λ (√(1+t^2 ))dt=[((ln ((√(1+t^2 ))+t)+t(√(1+t^2 )))/2)]_0 ^λ =((ln ((√(1+λ^2 ))+λ)+λ(√(1+λ^2 )))/2) ∫_0 ^λ t^2 (√(1+t^2 ))dt=[((t(2t^2 +1)(√(1+t^2 ))−ln ((√(1+t^2 ))+t))/8)]_0 ^λ =((λ(2λ^2 +1)(√(1+λ^2 ))−ln ((√(1+λ^2 ))+λ))/8) h_S =(L/(4λ))×((∫_0 ^λ t^2 (√(1+t^2 ))dt)/(∫_0 ^λ (√(1+t^2 ))dt)) =(L/(4λ))×((λ(2λ^2 +1)(√(1+λ^2 ))−ln ((√(1+λ^2 ))+λ))/8)×(2/(ln ((√(1+λ^2 ))+λ)+λ(√(1+λ^2 )))) =(L/(16))×(((2λ^2 +1)(√(1+λ^2 ))−((ln ((√(1+λ^2 ))+λ))/λ))/((√(1+λ^2 ))+((ln ((√(1+λ^2 ))+λ))/λ))) ⇒(h_S /H)=(1/(4λ))[((2(1+λ^2 )^(3/2) )/((√(1+λ^2 ))+((ln ((√(1+λ^2 ))+λ))/λ)))−1]](Q71594.png) | ||
| ||