
Question and Answers Forum
Question Number 7193 by peter james last updated on 15/Aug/16

Commented by Yozzia last updated on 15/Aug/16
![S(n)=1+2^2 −3^3 +4+5^2 −6^3 +7+8^2 −9^3 +... +[(3n−2)+(3n−1)^2 −(3n)^3 ] S(t=3n)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ] In grouping the terms of S(n) in threes, t=3n is the total number of terms in the sum−expression of S(n). If we require 3n−1 terms, we can write S(t=3n−1)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ]+27n^3 where n−1≡ −1 (mod 3) If we require 3n−2 terms, we write S(t=3n−2)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ]+27n^3 −(3n−1)^2 where n−2≡ −2 (mod 3). So, S(t)= { ((S(t=3n) )),((S(t=3n−1)=S(t=3n)+27n^3 )),((S(t=3n−2)=S(t=3n)+27n^3 −(3n−1)^2 )) :} t=number of terms −−−−−−−−−−−−−−−−−−−−−−−−−− (3k−2)+(3k−1)^2 −27k^3 =3k−2+9k^2 −6k+1−27k^3 =9k^2 −1−3k−27k^3 Using : Σ_(k=1) ^n 1=n , Σ_(k=1) ^n k=((n(n+1))/2) Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) , Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4), S(n)=9×((n(n+1)(2n+1))/6)−n−((3n(n+1))/2)−((27n^2 (n+1)^2 )/4) S(n)=((3n(n+1)(2n+1))/2)−n−((3n(n+1))/2)−((27n^2 (n+1)^2 )/4) S(n)=(n/8)[12(n+1)(2n+1)−8−12(n+1)−54n(n+1)^2 ] S(n)=(n/8)[12(n+1)(2n+1−1)−8−54n(n+1)^2 ] S(n)=(n/8)[24n^2 +24n−8−54n^3 −108n^2 −54n] S(n)=(n/8)[−8−54n^3 −84n^2 −30n] S(n)=−(n/4)(27n^3 +42n^2 +15n+4) n=1⇒S(3)=((−1)/4)(27+42+15+4)=−22 (3 terms) n=2⇒ S(6)=((−1)/2)(27×8+42×4+15×2+4)=−209 (6 terms) t=5⇒S(5)=−209+6^3 =7=1+2^2 −3^3 +4+5^2 −−−−−−−−−−−−−−−−−−−−−−−− So, S(t)= { ((((−n)/4)(27n^3 +42n^2 +15n+4) t≡ 0 (mod 3) )),((((−n)/4)(27n^3 +42n^2 +15n+4)+27n^3 t≡ −1 (mod 3) )),((((−n(27n^3 +42n^2 +15n+4))/4)+27n^3 −(3n−1)^2 t≡ −2 (mod 3) )) :}](Q7195.png)
Commented by peter james last updated on 16/Aug/16
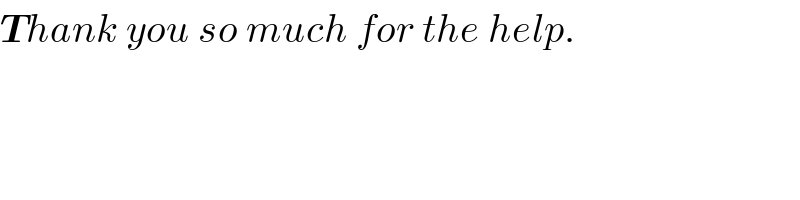
| ||
Question and Answers Forum | ||
Question Number 7193 by peter james last updated on 15/Aug/16 | ||
 | ||
Commented by Yozzia last updated on 15/Aug/16 | ||
![S(n)=1+2^2 −3^3 +4+5^2 −6^3 +7+8^2 −9^3 +... +[(3n−2)+(3n−1)^2 −(3n)^3 ] S(t=3n)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ] In grouping the terms of S(n) in threes, t=3n is the total number of terms in the sum−expression of S(n). If we require 3n−1 terms, we can write S(t=3n−1)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ]+27n^3 where n−1≡ −1 (mod 3) If we require 3n−2 terms, we write S(t=3n−2)=Σ_(k=1) ^n [(3k−2)+(3k−1)^2 −(3k)^3 ]+27n^3 −(3n−1)^2 where n−2≡ −2 (mod 3). So, S(t)= { ((S(t=3n) )),((S(t=3n−1)=S(t=3n)+27n^3 )),((S(t=3n−2)=S(t=3n)+27n^3 −(3n−1)^2 )) :} t=number of terms −−−−−−−−−−−−−−−−−−−−−−−−−− (3k−2)+(3k−1)^2 −27k^3 =3k−2+9k^2 −6k+1−27k^3 =9k^2 −1−3k−27k^3 Using : Σ_(k=1) ^n 1=n , Σ_(k=1) ^n k=((n(n+1))/2) Σ_(k=1) ^n k^2 =((n(n+1)(2n+1))/6) , Σ_(k=1) ^n k^3 =((n^2 (n+1)^2 )/4), S(n)=9×((n(n+1)(2n+1))/6)−n−((3n(n+1))/2)−((27n^2 (n+1)^2 )/4) S(n)=((3n(n+1)(2n+1))/2)−n−((3n(n+1))/2)−((27n^2 (n+1)^2 )/4) S(n)=(n/8)[12(n+1)(2n+1)−8−12(n+1)−54n(n+1)^2 ] S(n)=(n/8)[12(n+1)(2n+1−1)−8−54n(n+1)^2 ] S(n)=(n/8)[24n^2 +24n−8−54n^3 −108n^2 −54n] S(n)=(n/8)[−8−54n^3 −84n^2 −30n] S(n)=−(n/4)(27n^3 +42n^2 +15n+4) n=1⇒S(3)=((−1)/4)(27+42+15+4)=−22 (3 terms) n=2⇒ S(6)=((−1)/2)(27×8+42×4+15×2+4)=−209 (6 terms) t=5⇒S(5)=−209+6^3 =7=1+2^2 −3^3 +4+5^2 −−−−−−−−−−−−−−−−−−−−−−−− So, S(t)= { ((((−n)/4)(27n^3 +42n^2 +15n+4) t≡ 0 (mod 3) )),((((−n)/4)(27n^3 +42n^2 +15n+4)+27n^3 t≡ −1 (mod 3) )),((((−n(27n^3 +42n^2 +15n+4))/4)+27n^3 −(3n−1)^2 t≡ −2 (mod 3) )) :}](Q7195.png) | ||
Commented by peter james last updated on 16/Aug/16 | ||
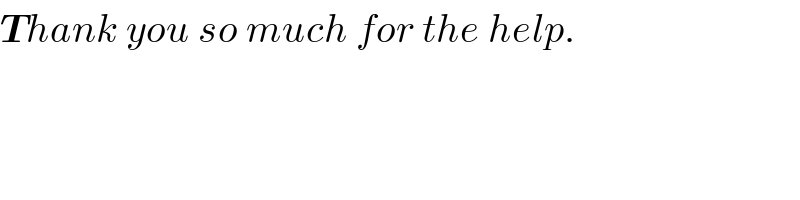 | ||