
Question and Answers Forum
Question Number 74446 by rajesh4661kumar@gmail.com last updated on 24/Nov/19
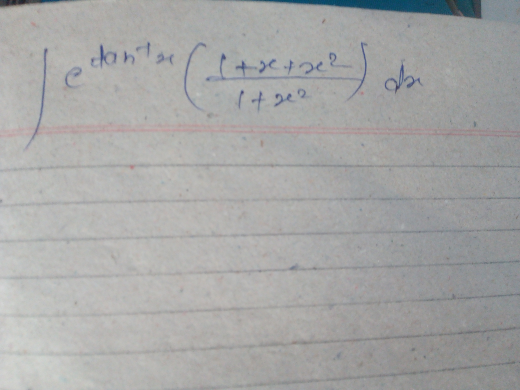
Answered by Kunal12588 last updated on 24/Nov/19
![I=∫e^(tan^(−1) x) (((1+x+x^2 )/(1+x^2 )))dx let t=tan^(−1) x ⇒dt=(dx/(1+x^2 )) I=∫e^t (1+tan t + tan^2 t)dt ⇒I=∫e^t (tan t + sec^2 t)dt ⊛ ⇒I=e^t tan t +C ⇒I=xe^(tan^(−1) x) +C ⊛ ∫e^x [f(x)+f ′(x)]dx=e^x f(x)+C](Q74452.png)
Commented by Kunal12588 last updated on 24/Nov/19
![∫e^x [f(x)+f ′(x)]dx =∫e^x f(x)dx+∫e^x f ′(x) dx =e^x f(x)−∫e^x f ′(x)dx+∫e^x f ′(x)dx =e^x f(x)+C](Q74454.png)
| ||
Question and Answers Forum | ||
Question Number 74446 by rajesh4661kumar@gmail.com last updated on 24/Nov/19 | ||
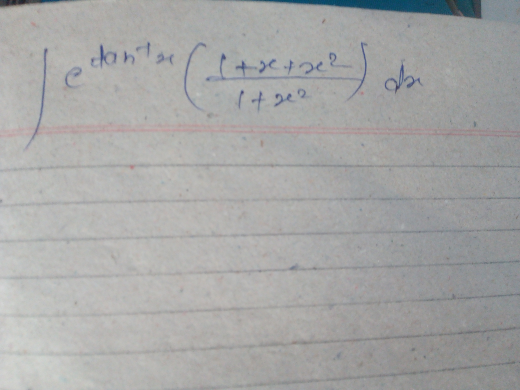 | ||
Answered by Kunal12588 last updated on 24/Nov/19 | ||
![I=∫e^(tan^(−1) x) (((1+x+x^2 )/(1+x^2 )))dx let t=tan^(−1) x ⇒dt=(dx/(1+x^2 )) I=∫e^t (1+tan t + tan^2 t)dt ⇒I=∫e^t (tan t + sec^2 t)dt ⊛ ⇒I=e^t tan t +C ⇒I=xe^(tan^(−1) x) +C ⊛ ∫e^x [f(x)+f ′(x)]dx=e^x f(x)+C](Q74452.png) | ||
| ||
Commented by Kunal12588 last updated on 24/Nov/19 | ||
![∫e^x [f(x)+f ′(x)]dx =∫e^x f(x)dx+∫e^x f ′(x) dx =e^x f(x)−∫e^x f ′(x)dx+∫e^x f ′(x)dx =e^x f(x)+C](Q74454.png) | ||