Math Question and Answers


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 74473 by arkanmath7@gmail.com last updated on 24/Nov/19

Commented by mathmax by abdo last updated on 24/Nov/19

$∣ z - 1 ∣= 1 \Rightarrow z - 1 = e^{i θ} 0 ⩽ θ ⩽ π \Rightarrow z = 1 + e^{i θ}$ $\int_{C} {(\bar{z})}^{2} d z = \int_{0}^{2 π} {(1 + e^{- i θ})}^{2} i e^{i θ} d θ$ $= i \int_{0}^{2 π} (1 + 2 e^{- i θ} + e^{- 2 i θ}) e^{i θ} d θ$ $= i \int_{0}^{2 π} (e^{i θ} + 2 + e^{- i θ}) d θ = i \int_{0}^{2 π} (e^{i θ} + e^{- i θ}) d θ + 2 i \int_{0}^{2 π} d θ$ $= 2 i \int_{0}^{2 π} c o s θ d θ + 4 i π = 2 i {[s i n θ]}_{0}^{2 π} + 4 i π = 0 + 4 i π = 4 i π$
Commented by mathmax by abdo last updated on 24/Nov/19

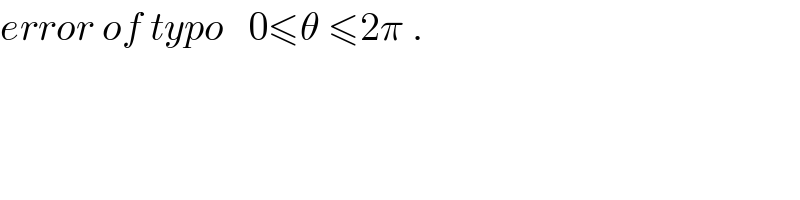
$e r r o r o f t y p o 0 ⩽ θ ⩽ 2 π .$
	Answered by mind is power last updated on 24/Nov/19
	${z∈C,∣z−1∣=1}={1+e^(it) ,t∈[0,2π]} ∫_C z^2^− dz=∫_0 ^(2π) (1+e^(−it) )^2 .ie^(it) dt =∫i(1+e^(−2it) +2e^(−it) )e^(it) dt =i∫_0 ^(2π) (e^(it) +e^(−it) +2)dt =4iπ$
	${z \in C, ∣ z - 1 ∣= 1} = {1 + e^{i t}, t \in [0, 2 π]}$ $\int_{C} z^{\bar{2}} d z = \int_{0}^{2 π} {(1 + e^{- i t})}^{2} . {i e}^{i t} d t$ $= \int i (1 + e^{- 2 i t} + 2 e^{- i t}) e^{i t} d t$ $= i \int_{0}^{2 π} (e^{i t} + e^{- i t} + 2) d t$ $= 4 i π$
	Commented by arkanmath7@gmail.com last updated on 24/Nov/19

	$t h n x$ $a f t e r I p o s t e d i t, I s o l v e d i t .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum