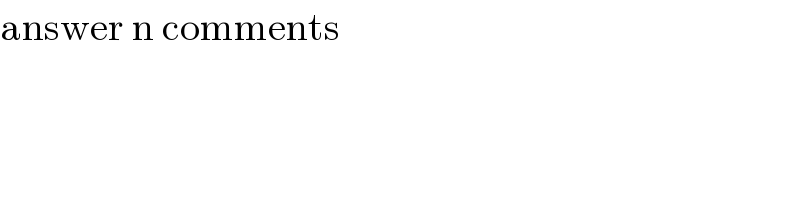Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7903 by tawakalitu last updated on 24/Sep/16

Commented by sou1618 last updated on 24/Sep/16

$$S=\frac{\underset{k=1}{\sum ^{99}}\sqrt{10+\sqrt{k}}}{\underset{k=1}{\sum ^{99}}\sqrt{10-\sqrt{k}}}$$$$S\fallingdotseq S{}^{\prime }=\frac{{\int }_0^{100}\sqrt{10+\sqrt{x}}dx}{{\int }_0^{100}\sqrt{10-\sqrt{y}}dy}$$$$t=10+\sqrt{x}$$$$x={(t-10)}^2$$$$dx=2t-20dt$$$$x(0\to 100)\iff t(10\to 20)$$$$$$$$u=10-\sqrt{y}$$$$y={(10-u)}^2$$$$dy=2t-20du$$$$y(0\to 100)\iff u(10\to 0)$$$$$$$$S{}^{\prime }=\frac{{\int }_{10}^{20}\sqrt{10+\sqrt{{(t-10)}^2}}(2t-20)dt}{{\int }_{10}^0\sqrt{10-\sqrt{{(10-u)}^2}}(2u+20)du}$$$$=\frac{{\int }_{10}^{20}\sqrt{10+\mid t-10\mid }(2t-20)dt}{{\int }_{10}^0\sqrt{10-\mid 10-u\mid }(2u-20)du}$$$$=\frac{{\int }_{10}^{20}2\sqrt{t}(t-10)dt}{{\int }_{10}^{0}2\sqrt{u}(u-10)du}$$$$=\frac{{\int }_{10}^{20}\sqrt{t^3}-10\sqrt{t}dt}{{\int }_{10}^0\sqrt{u^3}-10\sqrt{u}du}$$$$=\frac{{[\frac{2}{5}\sqrt{t^5}-10\frac{2}{3}\sqrt{t^3}]}_{10}^{20}}{{[\frac{2}{5}\sqrt{u^5}-10\frac{2}{3}\sqrt{u^3}]}_{10}^0}$$$$=\frac{\frac{2}{5}(\sqrt{{20}^5}-\sqrt{{10}^5})-10\frac{2}{3}(\sqrt{{20}^3}-\sqrt{{10}^3})}{0-(\frac{2}{5}\sqrt{{10}^5}-10\frac{2}{3}\sqrt{{10}^3})}\times \frac{3\sqrt{10}}{3\sqrt{10}}$$$$=\frac{\frac{6}{5}(4000\sqrt{2}-1000)-20(200\sqrt{2}-100)}{-\frac{6}{5}\left(1000\right)+20\left(100\right)}$$$$=\frac{4800\sqrt{2}-1200-4000\sqrt{2}+2000}{-1200+2000}$$$$=\frac{800\sqrt{2}+800}{800}$$$$=1+\sqrt{2}$$$$so$$$$S\fallingdotseq 1+\sqrt{2}$$

Commented by tawakalitu last updated on 24/Sep/16

$$Wowthankssomuch.ireallyappreciate.$$

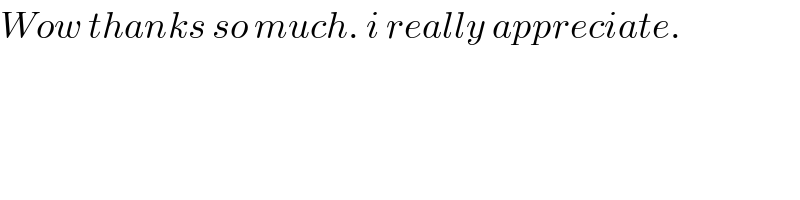
Commented by Yozzia last updated on 24/Sep/16

$$HowcomeS\fallingdotseq S{}^{\prime }?$$

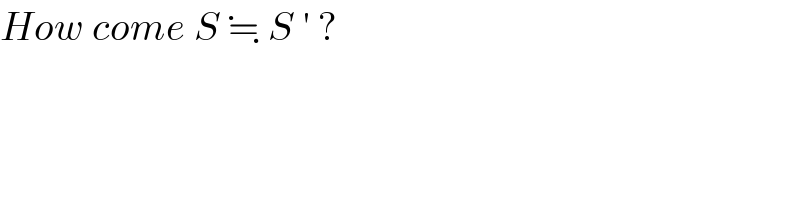
Commented by sou1618 last updated on 24/Sep/16

$$\sqrt{10\pm \sqrt{k}}\fallingdotseq {\int }_{k-1}^k\sqrt{10\pm \sqrt{x}}dx$$$$\underset{k=1}{\sum ^{100}}\sqrt{10\pm \sqrt{k}}\fallingdotseq \underset{k=1}{\sum ^{100}}{\int }_{k-1}^k\sqrt{10\pm \sqrt{x}}dx$$$$\left(\underset{k=1}{\sum ^{99}}\sqrt{10\pm \sqrt{k}}\right)+\sqrt{10\pm 10}\fallingdotseq {\int }_0^{100}\sqrt{10\pm \sqrt{x}}dx$$$$now$$$$\underset{k=1}{\sum ^{99}}\sqrt{10\pm \sqrt{k}}>>\sqrt{10\pm 10}$$$$Ithink\sqrt{10+10}islessthan\sqrt{2}\mathrm{\%}of\mathrm{\Sigma }$$$$because...when0<k<100$$$$\sqrt{2}\sqrt{10+\sqrt{k}}>\sqrt{10+10}$$$$$$$$$$$$\underset{k=1}{\sum ^{99}}\sqrt{10\pm \sqrt{k}}\fallingdotseq {\int }_0^{100}\sqrt{10\pm \sqrt{x}}dx$$$$so$$$$S\fallingdotseq S{}^{\prime }$$

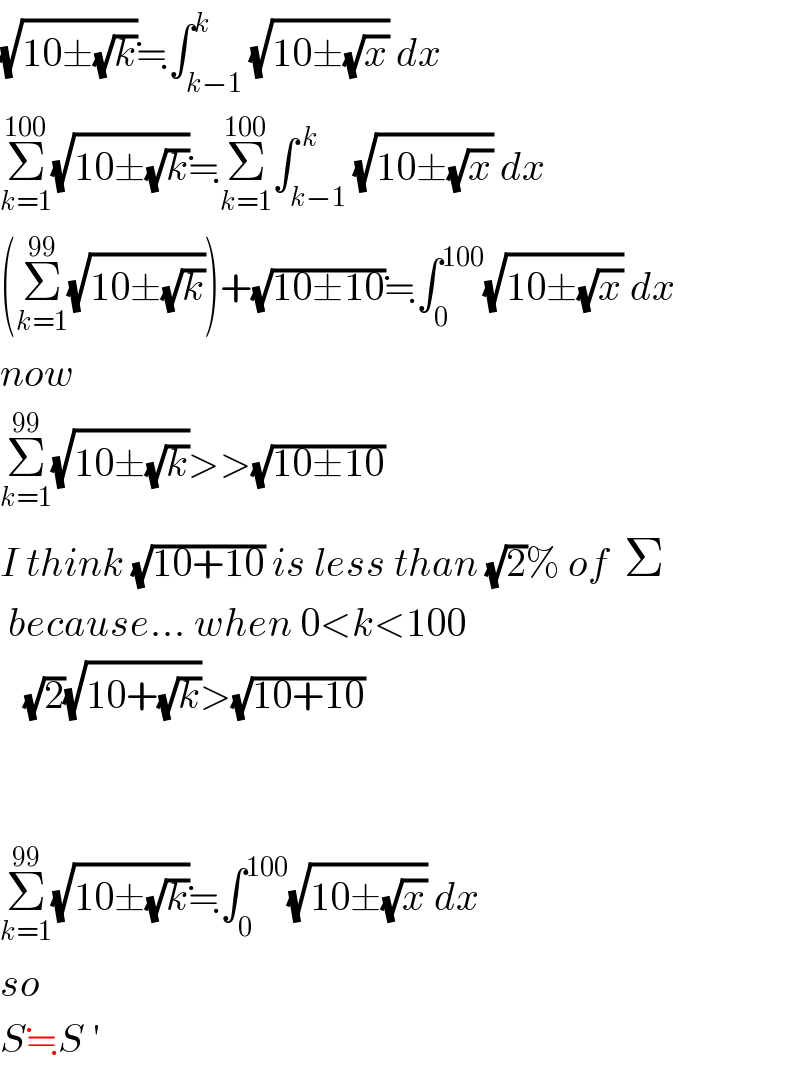
Answered by prakash jain last updated on 02/Oct/16

$$\mathrm{answer}\mathrm{n}\mathrm{comments}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com