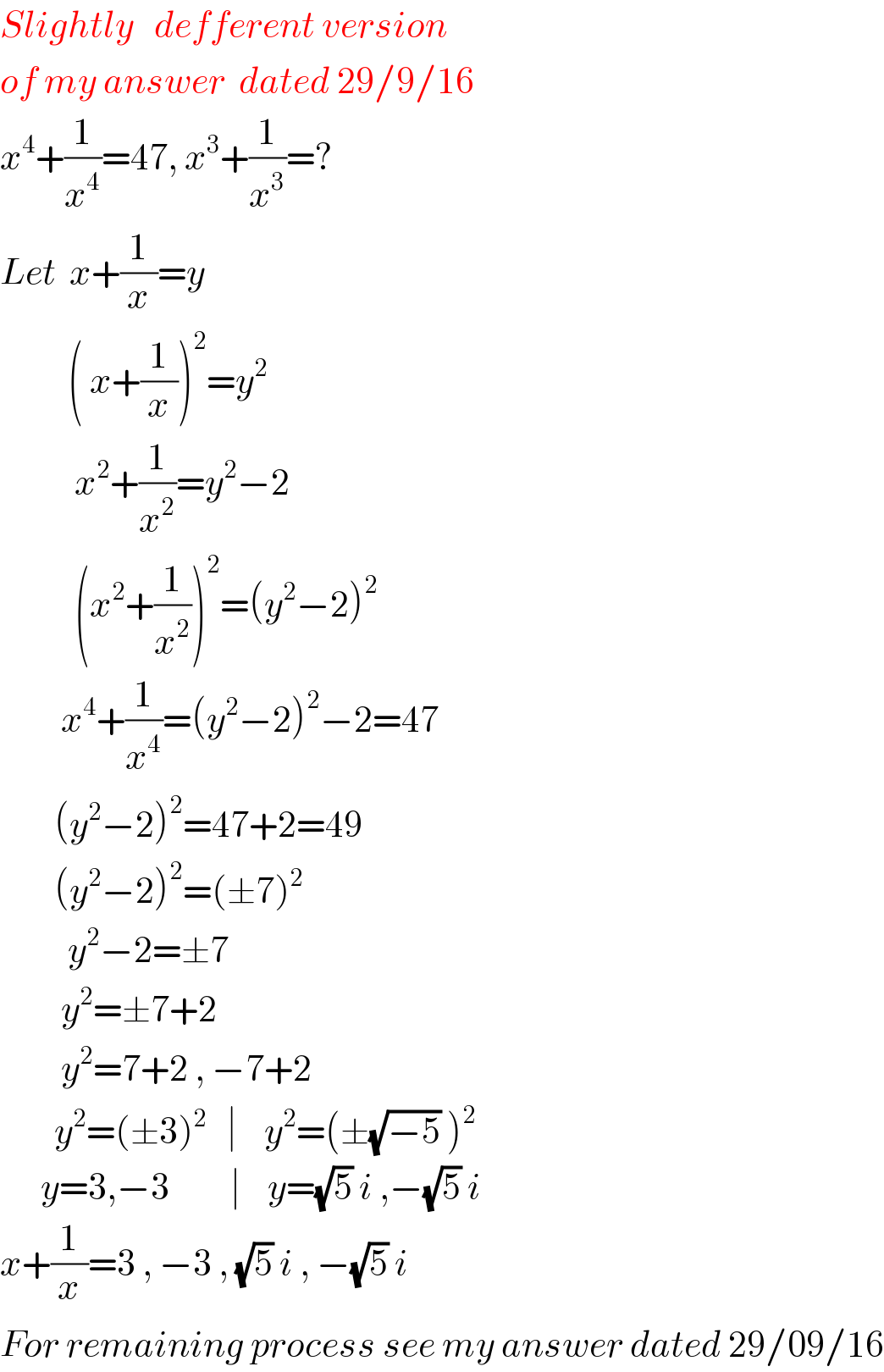Question and Answers Forum
Question Number 8073 by 314159 last updated on 29/Sep/16

Commented by 123456 last updated on 30/Sep/16
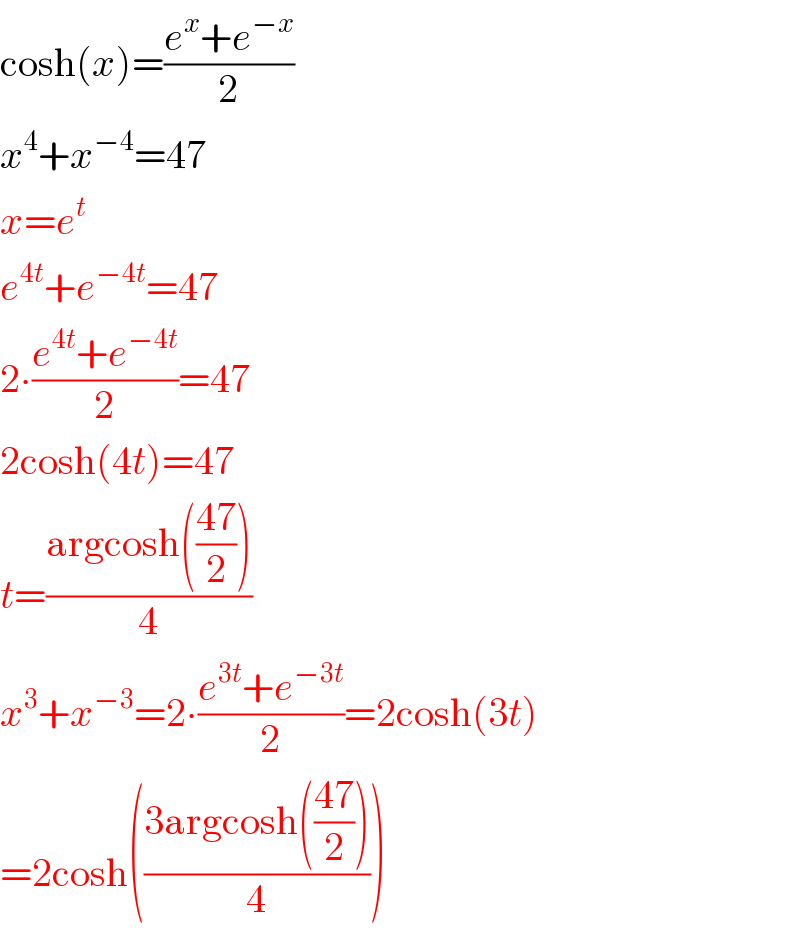
Commented by Rasheed Soomro last updated on 30/Sep/16

Commented by prakash jain last updated on 30/Sep/16
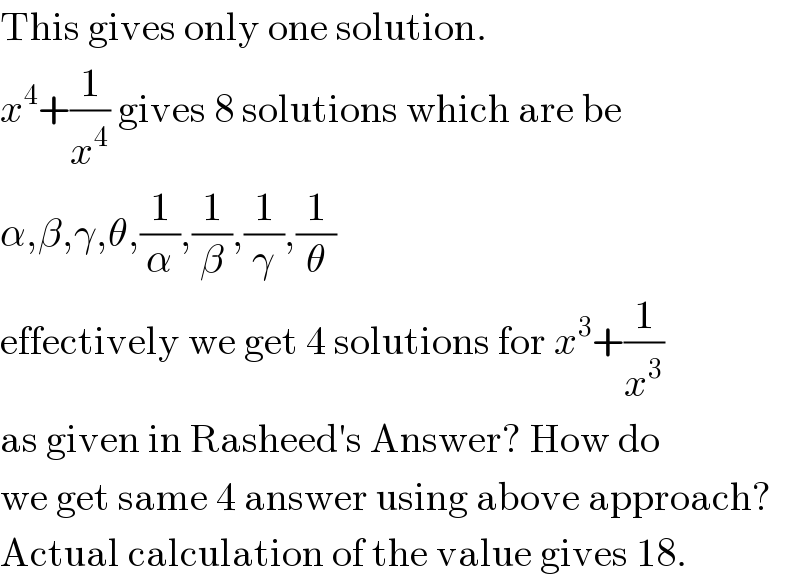
Commented by 123456 last updated on 30/Sep/16
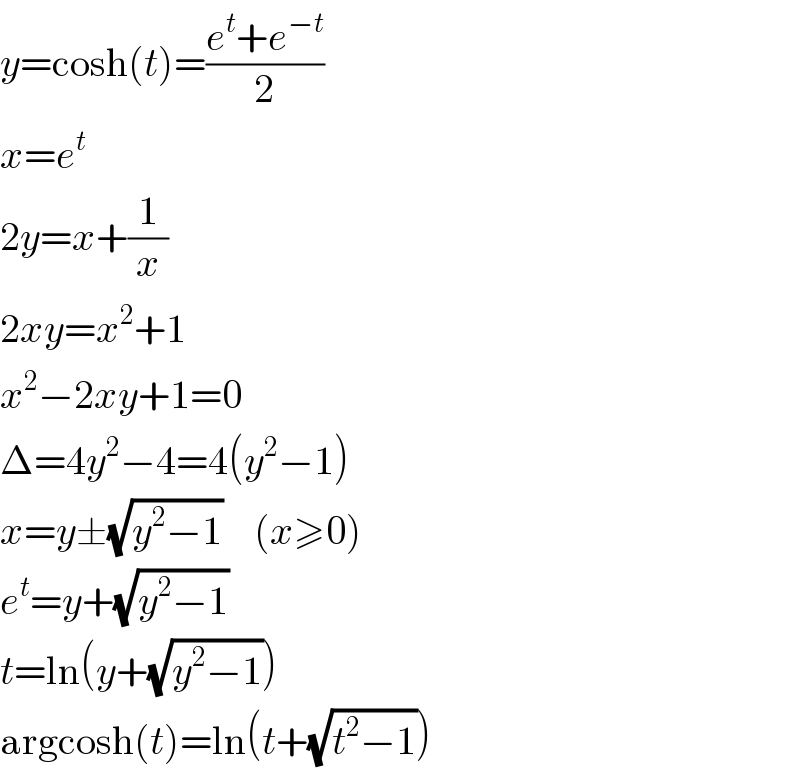
Commented by 123456 last updated on 30/Sep/16

Commented by prakash jain last updated on 30/Sep/16
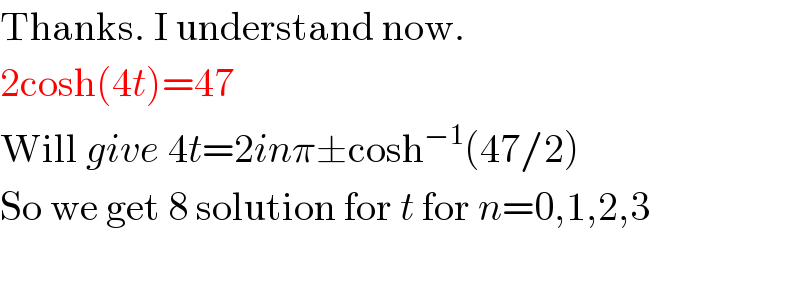
Answered by Rasheed Soomro last updated on 29/Sep/16
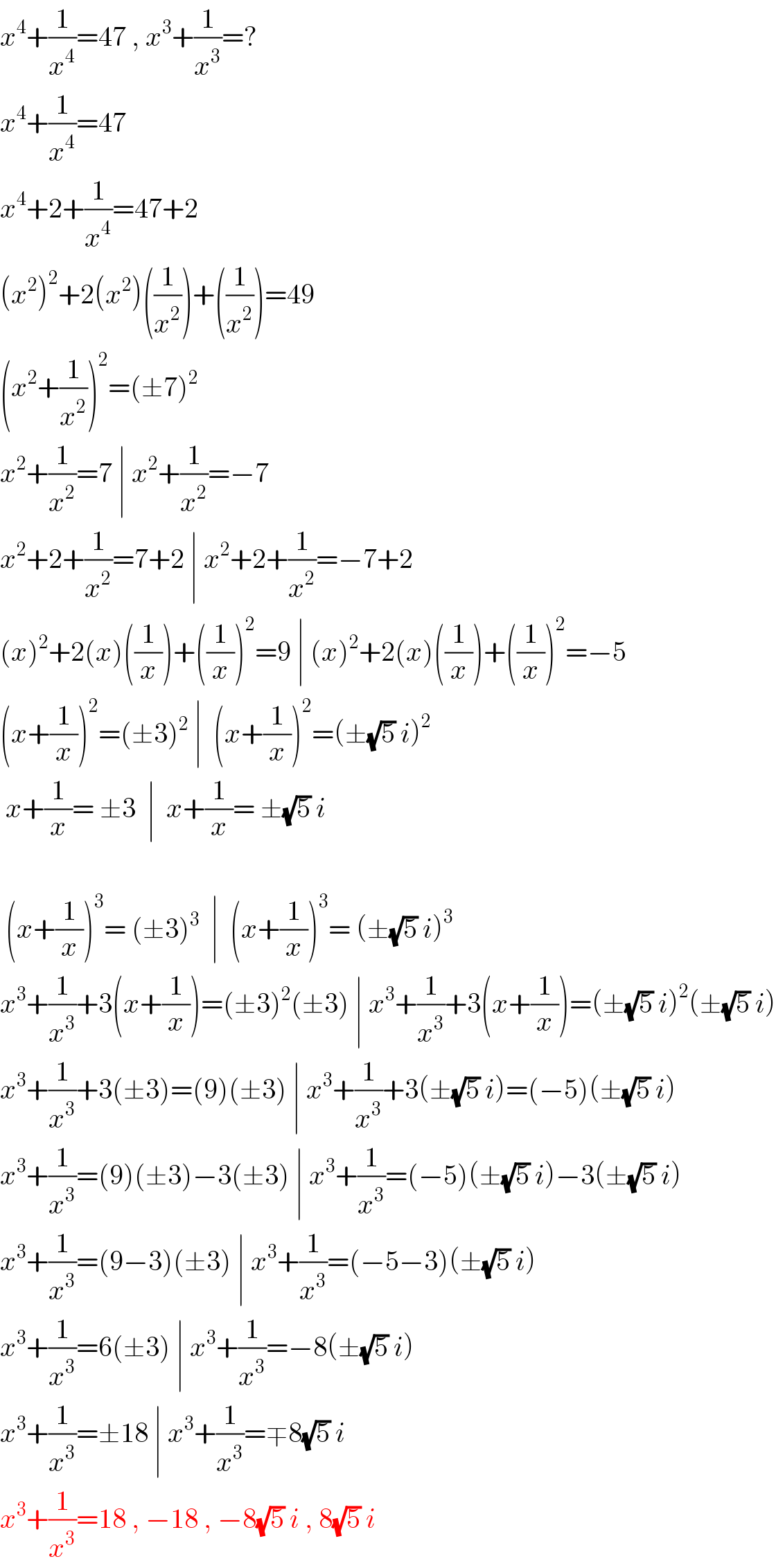
Answered by prof.kerdus last updated on 29/Sep/16

Answered by Rasheed Soomro last updated on 30/Sep/16
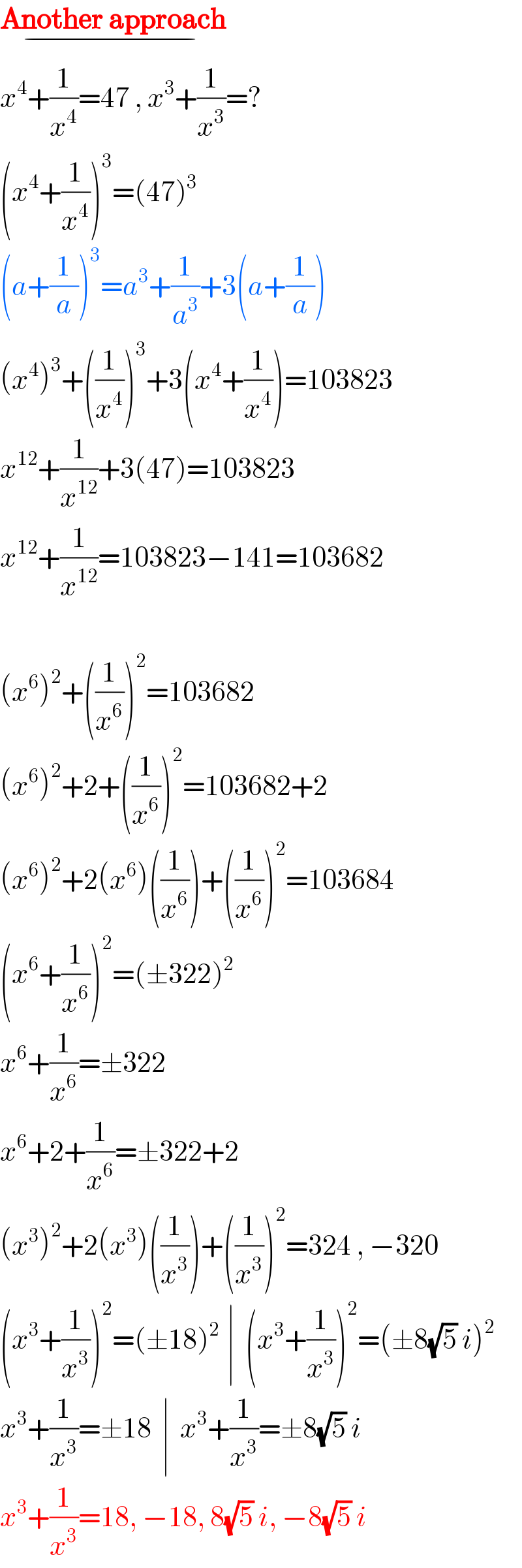
Answered by Rasheed Soomro last updated on 30/Sep/16