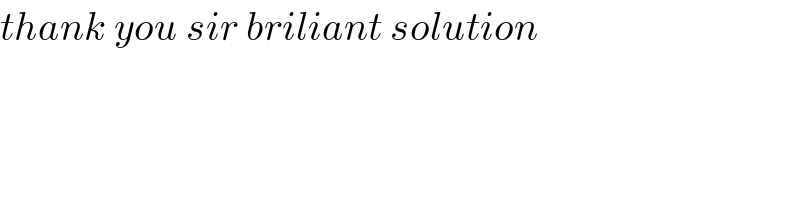Math Question and Answers


Question and Answers Forum

All Questions Topic List
Arithmetic Questions
Previous in All Question Next in All Question
Previous in Arithmetic Next in Arithmetic
Question Number 80786 by M±th+et£s last updated on 06/Feb/20

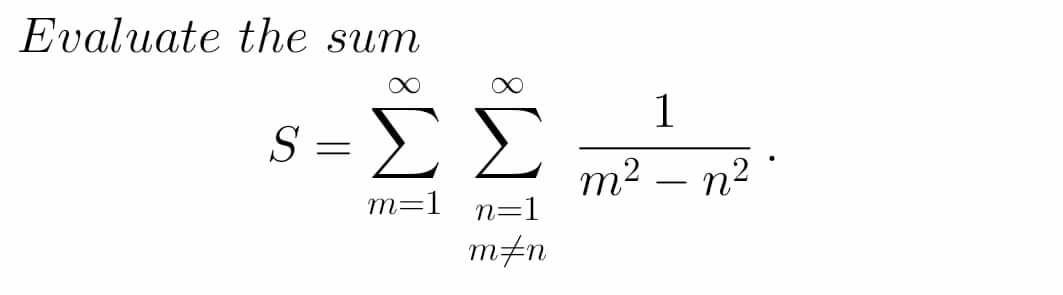
Commented by mind is power last updated on 06/Feb/20

$i w i l l t r y n o t e a s y!$
Commented by mr W last updated on 06/Feb/20

$i t h i n k {i t}^{'} s z e r o d u e t o s y m m e t r y .$ $S_{k} = \underset{m = 1}{\sum^{k}} \underset{\underset{n \neq m}{n = 1}}{\sum^{k}} \frac{1}{m^{2} - n^{2}} = 0$ $s i n c e f o r a p a i r (m = i a n d n = j) t h e r e$ $i s a c o r r e s p o n d i n g p a i r (m = j a n d$ $n = i) :$ $\frac{1}{i^{2} - j^{2}} + \frac{1}{j^{2} - i^{2}} = 0$ $S = \underset{m = 1}{\sum^{\infty}} \underset{\underset{n \neq m}{n = 1}}{\sum^{\infty}} \frac{1}{m^{2} - n^{2}} = \lim_{k \to \infty} S_{k} = 0$
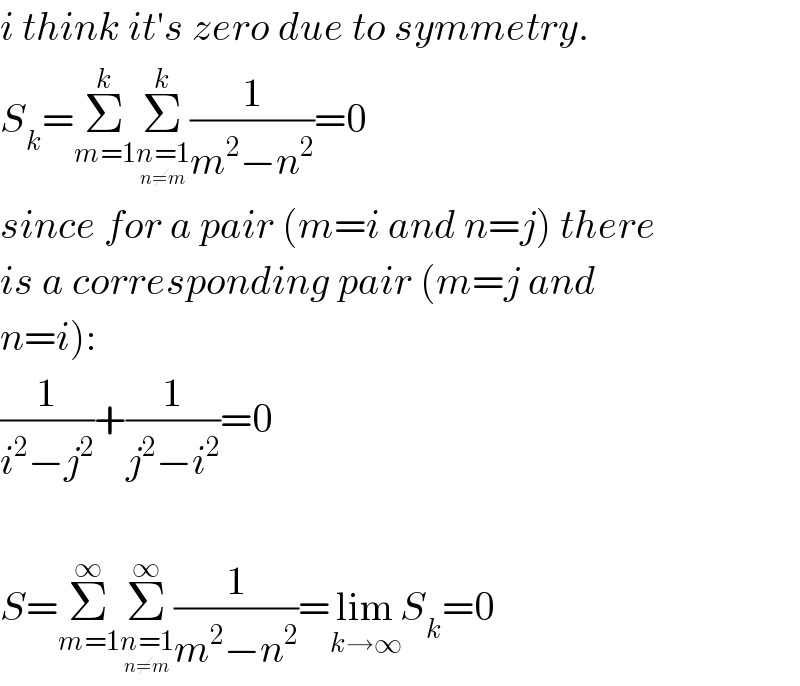
Commented by mr W last updated on 06/Feb/20

$t h e q u e s t i o n c a n b e m o d i f i e d t o$ $S = \underset{m = 1}{\sum^{\infty}} \underset{n = 1}{\sum^{\infty}} \frac{1}{m^{2} + n^{2}} = ?$
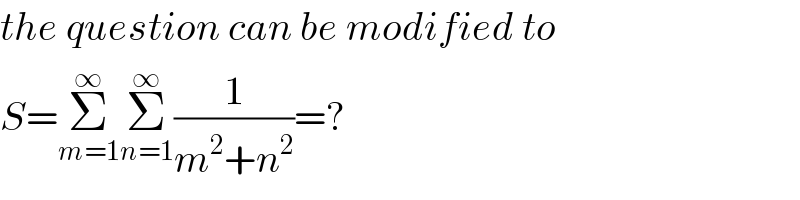
Commented by mathmax by abdo last updated on 06/Feb/20

$t r y t o p r o v e t h a t \sum_{n = 1 n \neq m}^{\infty} \frac{1}{n^{2} - m^{2}} = \frac{3}{4 m^{2}}$
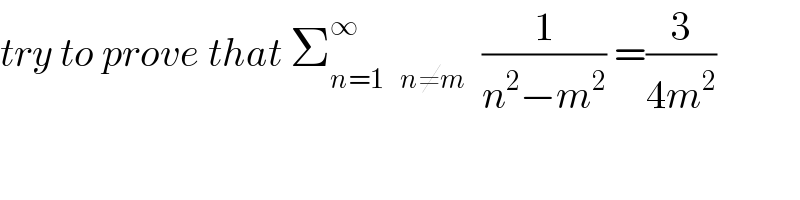
Commented by ~blr237~ last updated on 07/Feb/20

$l e t h (m) = \sum_{n \in N} \frac{1}{m^{2} + n^{2}}$ $l e t s t a t e f (z) = \frac{1}{m^{2} + z^{2}}, u s i n g t h e R e s i d u t h e o r e m$ $h (m) = - Σ R e s (f (z) π c o t (π z), z_{k})$ $h (m) = - (\frac{π c o t (i π m)}{2 i m} + \frac{π c o t (- i π m)}{- 2 i m})$ $h (m) = i π \frac{c o t (i π m)}{m} = \frac{π c o t h (π m)}{m}$ $S o, S = \underset{m = 1}{\sum^{\infty}} (\frac{1}{m^{2}} + \frac{π c o t h (π m)}{2 m})$ $S = ζ (2) + \frac{π}{2} \underset{m = 1}{\sum^{\infty}} \frac{c o t h (π m)}{m}$
	Answered by ~blr237~ last updated on 07/Feb/20

	$W e h a v e \forall m ⩾ 2 \underset{n \underset{n \neq m}{=} 1}{\sum^{\infty}} \frac{1}{m^{2} - n^{2}} = - \frac{3}{4 m^{2}} (l e t p r o v e)$ $f (m) = \underset{n = 1 n \neq m}{\sum^{\infty}} \frac{1}{m^{2} - n^{2}} . k n o w i n g \frac{1}{m^{2} - n^{2}} = - \frac{1}{2 m} (\frac{1}{n - m} - \frac{1}{n + m})$ $f (m) = - \frac{1}{2 m} [\underset{n = 1}{\sum^{m - 1}} (\frac{1}{n - m} - \frac{1}{n + m}) + \underset{n = m + 1}{\sum^{\infty}} (\frac{1}{n - m} - \frac{1}{n + m})]$ $f (m) = \frac{1}{2 m} [\underset{p = m + 1}{\sum^{2 m - 1}} \frac{1}{p} + \underset{p = 1}{\sum^{m - 1}} \frac{1}{p}] - \frac{1}{2 m} [\underset{p = 1}{\sum^{\infty}} (\frac{1}{p} - \frac{1}{p + 2 m})]$ $l e t s h o w t h a t g (m) = \underset{p = 1}{\sum^{\infty}} (\frac{1}{p} - \frac{1}{p + m}) = \underset{p = 1}{\sum^{m}} \frac{1}{p}$ $g (m) = \underset{p = 1}{\sum^{\infty}} (\underset{k = 0}{\sum^{m - 1}} (\frac{1}{p + k} - \frac{1}{p + k + 1}))$ $= \underset{k = 0}{\sum^{m - 1}} (\underset{p = 1}{\sum^{\infty}} (\frac{1}{k + p} - \frac{1}{k + p + 1}))$ $= \underset{k = 0}{\sum^{m - 1}} \frac{1}{k + 1} = \underset{k = 1}{\sum^{m}} \frac{1}{k}$ $S o,$ $f (m) = \frac{1}{2 m} (\underset{p = 1}{\sum^{2 m - 1}} \frac{1}{p} - \frac{1}{m}) - \frac{1}{2 m} \underset{p = 1}{\sum^{2 m}} \frac{1}{p}$ $f (m) = - \frac{1}{2 m^{2}} - \frac{1}{2 m} \times \frac{1}{2 m} = - \frac{3}{4 m^{2}}$ $F i n a l l y S = \underset{m = 1}{\sum^{\infty}} f (m) = - \frac{3}{4} ζ (2) = - \frac{π^{2}}{8}$
	Commented by M±th+et£s last updated on 07/Feb/20

	$i t h i n k t h a t {i t}^{^{'}} s \frac{- π^{2}}{8}$
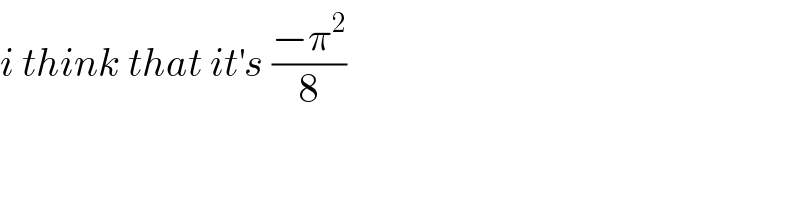
	Commented by ~blr237~ last updated on 07/Feb/20

	$y e s {i t}^{'} s$
	Commented by M±th+et£s last updated on 07/Feb/20

	$t h a n k y o u s i r b r i l i a n t s o l u t i o n$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum