Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 83824 by Power last updated on 06/Mar/20

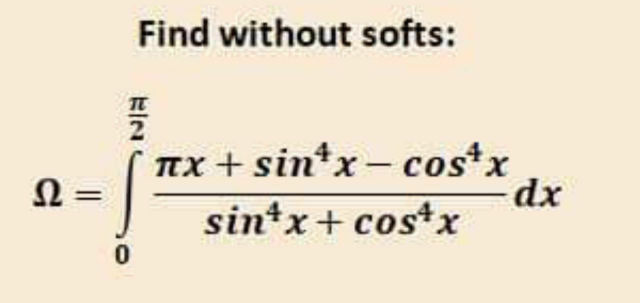
Commented by mathmax by abdo last updated on 06/Mar/20

$$changementx=\frac{\pi }{2}-tgive$$$$\mathrm{\Omega }=-{\int }_0^{\frac{\pi }{2}}\frac{\pi (\frac{\pi }{2}-t)+{cos}^{4}t-{sin}^{4}t}{{cos}^{4}t+{sin}^{4}t}(-dt)$$$$=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dt}{{cos}^{4}t+{sin}^{4}tdt}+{\int }_0^{\frac{\pi }{2}}\frac{-\pi t+{cos}^{4}t-{sin}^{4}t}{{cos}^{4}t+{sin}^{4}t}dt$$$$=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dt}{{cos}^{4}t+{sin}^{4}t}-\mathrm{\Omega }\Rightarrow 2\mathrm{\Omega }=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dt}{1-2{cos}^{2}t{sin}^{2}t}\Rightarrow$$$$\mathrm{\Omega }=\frac{{\pi }^2}{4}{\int }_0^{\frac{\pi }{2}}\frac{dt}{1-2{\left(\frac{sin\left(2t\right)}{2}\right)}^2}=\frac{{\pi }^2}{4}{\int }_0^{\frac{\pi }{2}}\frac{dt}{1-\frac{1}{2}{sin}^2\left(2t\right)}$$$$=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dt}{2-\frac{1-cos\left(4t\right)}{2}}={\pi }^2{\int }_0^{\frac{\pi }{2}}\frac{dt}{3+cos\left(4t\right)}$$$${=}_{4t=u}{\pi }^2{\int }_0^{2\pi }\frac{1}{3+cosu}\frac{du}{4}=\frac{{\pi }^2}{4}{\int }_0^{2\pi }\frac{du}{3+cosu}changement{e}^{iu}=z\Rightarrow$$$${\int }_0^{2\pi }\frac{du}{3+cosu}={\int }_{\mid z\mid =1}\frac{1}{3+\frac{z+z^{-1}}{2}}\frac{dz}{iz}$$$$={\int }_{\mid z\mid =1}\frac{2dz}{iz(6+z+z^{-1})}={\int }_{\mid z\mid =1}\frac{-2idz}{6z+z^2+1}letW\left(z\right)=\frac{-2i}{z^2+6z+1}$$$$polesofW?$$$${\mathrm{\Delta }}^{{}^{\prime }}=9-1=8\Rightarrow z_1=-3+2\sqrt{2}and{z}_2=-3-2\sqrt{2}\Rightarrow W\left(z\right)=\frac{-2i}{(z-z_1)(z-z_2)}$$$$\mid z_1\mid -1=\mid -3+2\sqrt{2}\mid -1=3-2\sqrt{2}-1=2-2\sqrt{2}<0\Rightarrow \mid z_1\mid <1$$$$\mid z_2\mid =3+2\sqrt{2}-1=2+2\sqrt{2}>1residustheoremgive$$$${\int }_{\mid z\mid =1}W\left(z\right)dz=2i\pi Res(W,z_1)=2i\pi \times \frac{-2i}{z_1-z_2}=\frac{4\pi }{4\sqrt{2}}=\frac{\pi }{\sqrt{2}}\Rightarrow$$$$\mathrm{\Omega }=\frac{{\pi }^2}{4}\times \frac{\pi }{\sqrt{2}}=\frac{{\pi }^3}{4\sqrt{2}}$$

Answered by TANMAY PANACEA last updated on 06/Mar/20

$$I={\int }_0^{\frac{\pi }{2}}\frac{\pi (\frac{\pi }{2}-x)+{sin}^4(\frac{\pi }{2}-x)-{cos}^4(\frac{\pi }{2}-x)}{{sin}^4(\frac{\pi }{2}-x)+{cos}^4(\frac{\pi }{2}-x)}dx$$$$2I={\int }_0^{\frac{\pi }{2}}\frac{\pi \left(\frac{\pi }{2}\right)}{{cos}^{4}x+{sin}^{4}x}$$$$2I=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{{sec}^{2}x\times (1+{tan}^{2}x)}{1+{tan}^{4}x}dx$$$$I=\frac{{\pi }^2}{4}{\int }_0^{\mathrm{\infty }}\frac{1+t^2}{1+t^4}dt[t=tanx]$$$$I=\frac{{\pi }^2}{4}{\int }_0^{\mathrm{\infty }}\frac{1+\frac{1}{t^2}}{t^2+\frac{1}{t^2}}dt$$$$=\frac{{\pi }^2}{4}{\int }_0^{\mathrm{\infty }}\frac{d(t-\frac{1}{t})}{{(t-\frac{1}{t})}^2+2}$$$$\frac{{\pi }^2}{4}\times \frac{1}{\sqrt{2}}\mid {tan}^{-1}\left(\frac{t-\frac{1}{t}}{\sqrt{2}}\right){\mid }_0^{\mathrm{\infty }}$$$$\frac{{\pi }^2}{4\sqrt{2}}\times \{({tan}^{-1}\mathrm{\infty }-{tan}^{-1}(-\mathrm{\infty })\}$$$$\frac{{\pi }^2}{4\sqrt{2}}\times (\frac{\pi }{2}+\frac{\pi }{2})=\frac{{\pi }^3}{4\sqrt{2}}$$$$\mathit{p}\mathit{l}\mathit{s}\mathit{c}\mathit{h}\mathit{e}\mathit{c}\mathit{k}$$

Commented by mathmax by abdo last updated on 06/Mar/20

$$youransweriscorrectsirtanmay$$

Commented by Power last updated on 06/Mar/20

$$\mathrm{thanks}$$

Commented by TANMAY PANACEA last updated on 06/Mar/20

$$thankyoubothofyousir$$

Answered by Kamel Kamel last updated on 07/Mar/20

$$Putt=\frac{\pi }{2}-x$$$$\therefore \mathrm{\Omega }={\int }_0^{\frac{\pi }{2}}\frac{\frac{{\pi }^2}{2}-\pi t+{cos}^4\left(t\right)-{sin}^4\left(t\right)}{{cos}^4\left(t\right)+{sin}^4\left(t\right)}dx$$$$\therefore 2\mathrm{\Omega }=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dx}{{cos}^4\left(x\right)+{sin}^4\left(x\right)}=\frac{{\pi }^2}{2}{\int }_0^{\frac{\pi }{2}}\frac{dx}{1-2{sin}^2\left(x\right){cos}^2\left(x\right)}$$$$=2{\pi }^2{\int }_0^{\frac{\pi }{2}}\frac{dx}{2-{sin}^2\left(2x\right)}\stackrel{t=2x}{=}{\pi }^2{\int }_0^{\pi }\frac{dt}{2-{sin}^2\left(t\right)}=2{\pi }^2{\int }_0^{\pi }\frac{dt}{cos\left(2t\right)+3}$$$$\stackrel{u=2t}{=}{\pi }^2{\int }_0^{2\pi }\frac{du}{cos\left(u\right)+3}={\pi }^2{\int }_{-\pi }^{\pi }\frac{du}{cos\left(u\right)+3}\stackrel{v=tg(\frac{u}{2}}{=}2{\pi }^2{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}\frac{dv}{1-v^2+3+3v^2}$$$$=2{\pi }^2{\int }_0^{+\mathrm{\infty }}\frac{dv}{v^2+2}=\frac{{\pi }^2}{\sqrt{2}}Arctg\left(\frac{v}{\sqrt{2}}\right){\mid }_0^{+\mathrm{\infty }}=\frac{{\pi }^3}{2\sqrt{2}}\Rightarrow \mathrm{\Omega }=\frac{{\pi }^3}{4\sqrt{2}}$$$$\therefore {\int }_0^{\frac{\pi }{2}}\frac{\pi x+{sin}^4\left(x\right)-{cos}^4\left(x\right)}{{sin}^4\left(x\right)+{cos}^4\left(x\right)}dx=\frac{{\pi }^3}{4\sqrt{2}}$$$$\mathit{K}\mathit{A}\mathit{M}\mathit{E}\mathit{L}\mathit{B}\mathit{E}\mathit{N}\mathit{A}\mathit{I}\mathit{C}\mathit{H}\mathit{A}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com