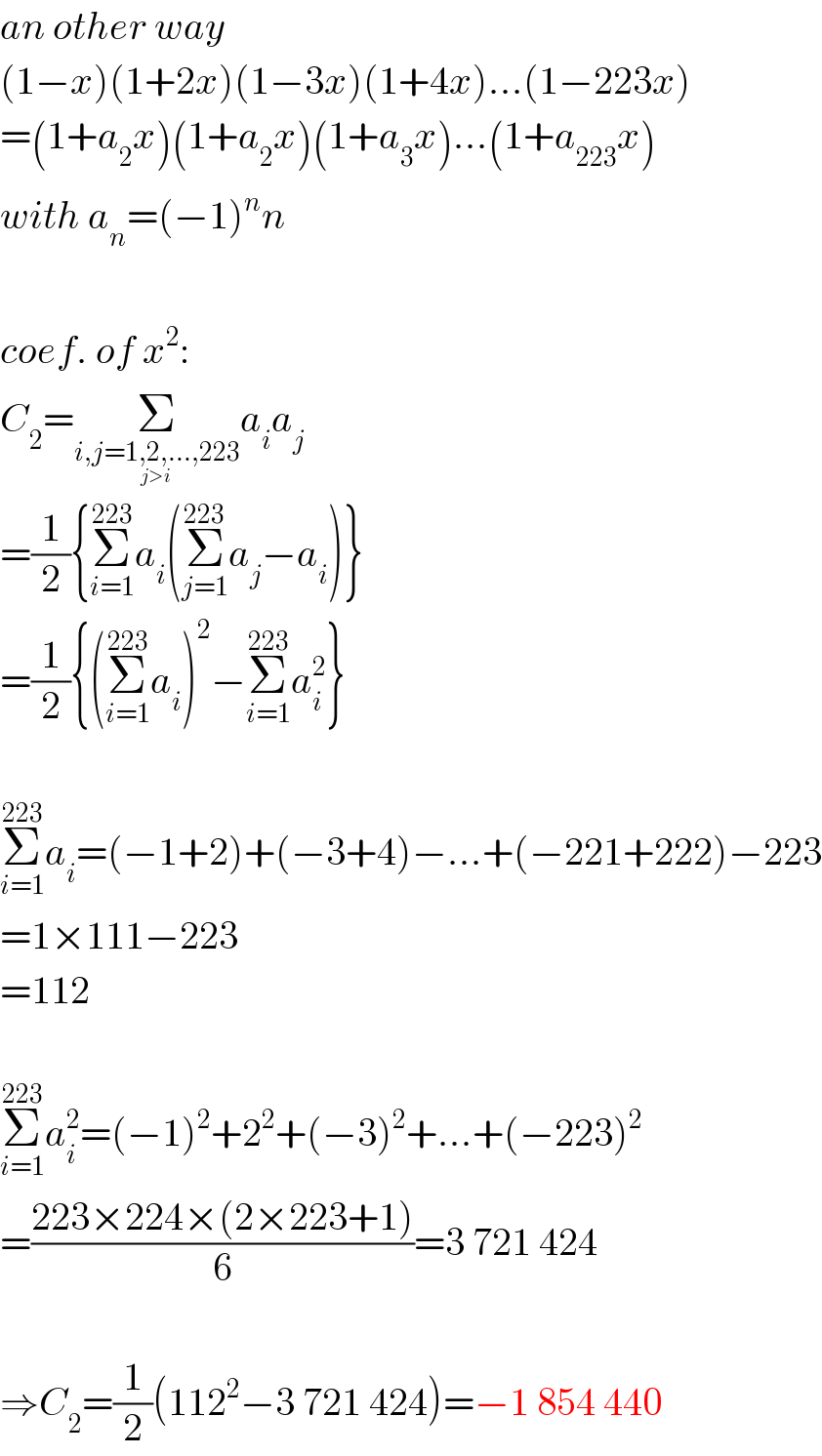Question and Answers Forum
Question Number 85365 by Power last updated on 21/Mar/20

Answered by jagoll last updated on 21/Mar/20
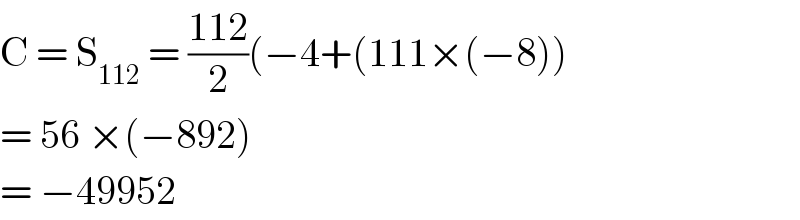
Commented by Power last updated on 21/Mar/20

Commented by john santu last updated on 21/Mar/20
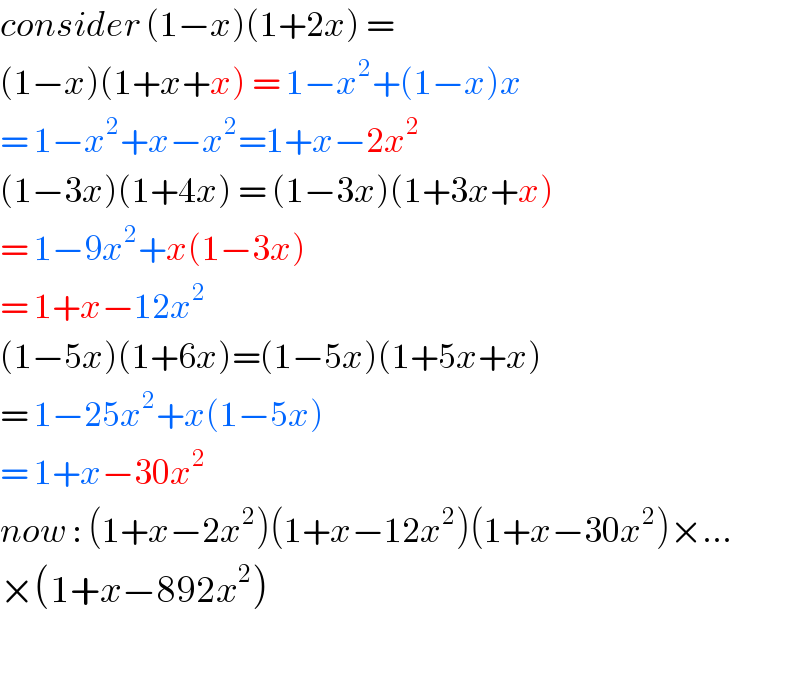
Commented by Power last updated on 21/Mar/20

Commented by john santu last updated on 21/Mar/20

Answered by mr W last updated on 21/Mar/20
}(1−223x) ={Π_(n=1) ^(111) [1+x−2n(2n−1)x^2 ]}(1−223x) coef. of x^2 : −Σ_(n=1) ^(111) 2n(2n−1)+((111×110)/2)−223×111 =−Σ_(n=1) ^(111) (4n^2 −2n)+((111×110)/2)−223×111 =−(4×((111×112×223)/6)−2×((111×112)/2))+((111×110)/2)−223×111 =−4×((111×112×223)/6)−56×111 =−1 854 440 ⇒ answer](Q85381.png)
Commented by Power last updated on 21/Mar/20

Answered by mr W last updated on 21/Mar/20