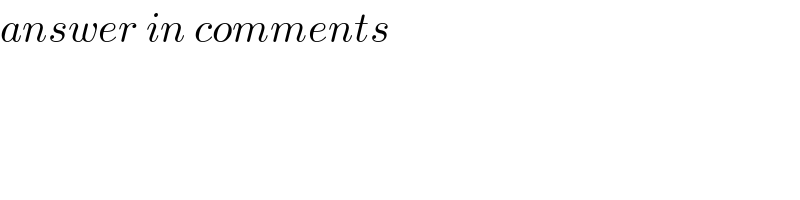Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 8558 by Sopheak last updated on 16/Oct/16

Commented by FilupSmith last updated on 16/Oct/16

$$S_n=\underset{k=1}{\sum ^n}\frac{k^4}{(2k-1)(2k+1)}$$$$\frac{1}{(2k-1)(2k+1)}=\frac{A}{2k-1}+\frac{B}{2k+1}$$$$1=A(2k+1)+B(2k-1)$$$$2kA+A+2kB-B=1$$$$2k(A+B)+A-B=1$$$$A+B=0$$$$A-B=1$$$$A=-B$$$$-2B=1\Rightarrow B=-\frac{1}{2}$$$$\therefore A=\frac{1}{2}$$$$$$$$\therefore \frac{1}{(2k-1)(2k+1)}=\frac{1}{2(2k-1)}+\frac{1}{2(2k+1)}$$$$\therefore \underset{k=1}{\sum ^n}\frac{k^4}{(2k-1)(2k+1)}=\frac{1}{2}\underset{k=1}{\sum ^n}{k}^4(\frac{1}{(2k-1)}+\frac{1}{(2k+1)})$$$$2S_n=\underset{k=1}{\sum ^n}\frac{k^4}{2k-1}+\underset{k=1}{\sum ^n}\frac{k^4}{2k+1}$$$$continue$$

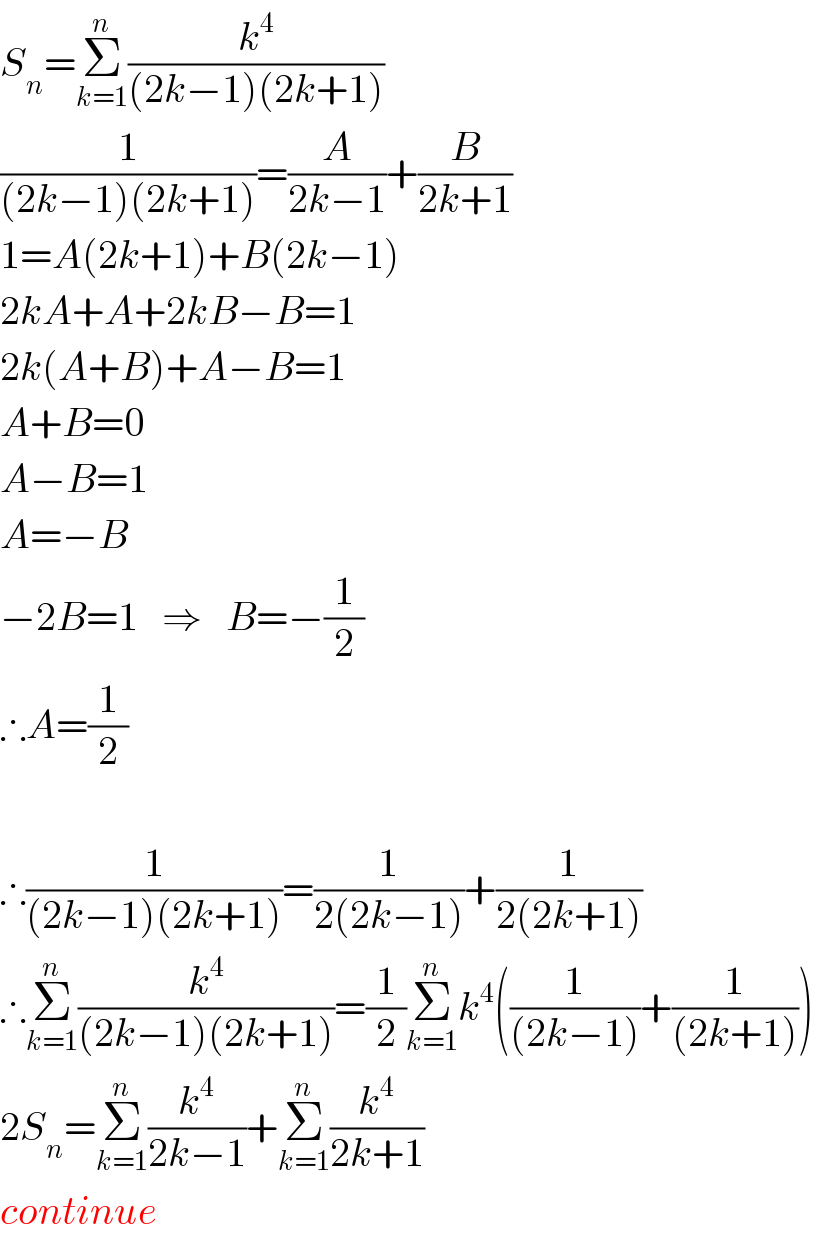
Commented by FilupSmith last updated on 16/Oct/16

$$\mathrm{For}\mathrm{reference},\mathrm{according}\mathrm{to}\mathrm{wolframAlpha}:$$$$S_n=\frac{n^4+2n^3+2n^2+n}{12n+6}$$

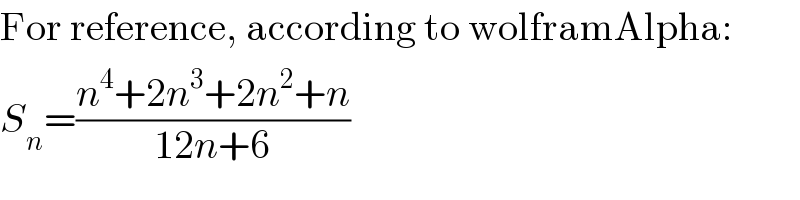
Commented by prakash jain last updated on 16/Oct/16

$$\frac{k^4}{(2k-1)(2k+1)}=\frac{1}{16}\left[\frac{16k^4-1+1}{(2k-1)(2k+1)}\right]$$$$=\frac{1}{16}[\frac{(4k^2-1)(4k^2+1)}{(2k-1)(2k+1)}+\frac{1}{(2k-1)(2k+1)}]$$$$=\frac{1}{16}[4k^2+1+\frac{1}{2}(\frac{1}{2k-1}-\frac{1}{2k+1})]$$$$\underset{k=1}{\sum ^n}\frac{k^4}{(2k-1)(2k+1)}=\frac{1}{16}\underset{k=1}{\sum ^n}4k^2+\frac{1}{16}\underset{k=1}{\sum ^n}1$$$$+\underset{k=1}{\sum ^n}(\frac{1}{2k-1}-\frac{1}{2k+1})$$$$\underset{k=1}{\sum ^n}(\frac{1}{2k-1}-\frac{1}{2k+1})=\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}..+\frac{1}{2n-1}-\frac{1}{2n+1}$$$$=1-\frac{1}{2n+1}=\frac{2n}{2n+1}$$$$\frac{1}{32}\underset{k=1}{\sum ^n}(\frac{1}{2k-1}-\frac{1}{2k+1})=\frac{n}{16(2n+1)}$$$$\frac{1}{16}\underset{k=1}{\sum ^n}4k^2=\frac{n(n+1)(2n+1)}{24}$$$$\frac{1}{16}\underset{k=1}{\sum ^n}1=\frac{n}{16}$$$$\underset{k=1}{\sum ^n}\frac{k^4}{(2k-1)(2k+1)}=\frac{n(n+1)(2n+1)}{24}+\frac{n}{16}+\frac{1}{16}\left(\frac{n}{2n+1}\right)$$$$=\frac{2n(n+1){(2n+1)}^2+3n(2n+1)+3n}{48(2n+1)}$$$$$$$$=\frac{(2n^2+2n)(4n^2+4n+1)+(6n^2+3n)+3n}{48(2n+1)}$$$$=\frac{8n^4+8n^3+8n^3+8n^2+2n^2+2n+6n^2+3n+3n}{48(2n+1)}$$$$=\frac{8n^4+16n^3+16n^2+8n}{48(2n+1)}=\frac{n^4+2n^3+2n^2+n}{6(2n+1)}$$

Answered by prakash jain last updated on 16/Oct/16

$$answerincomments$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com