
Question and Answers Forum
Question Number 85896 by ar247 last updated on 25/Mar/20

Commented by abdomathmax last updated on 25/Mar/20
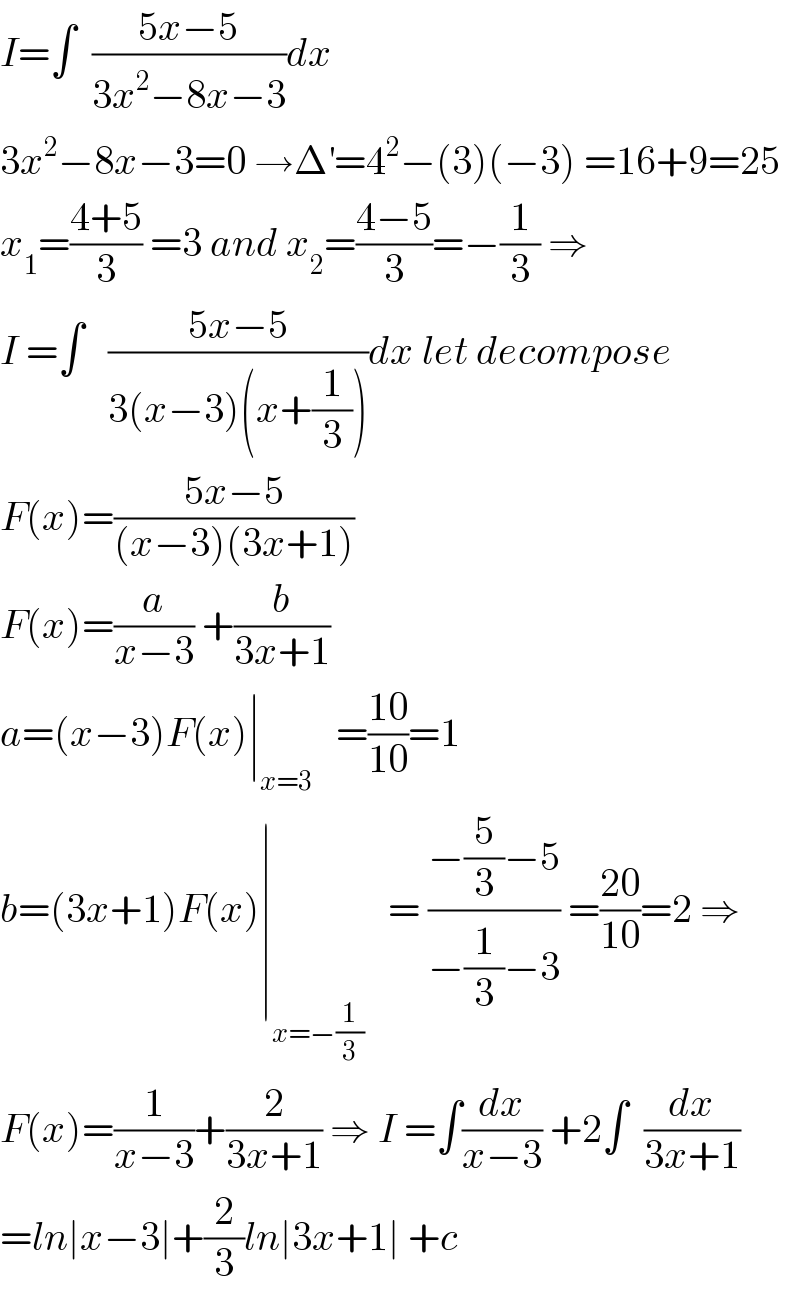
Commented by abdomathmax last updated on 25/Mar/20
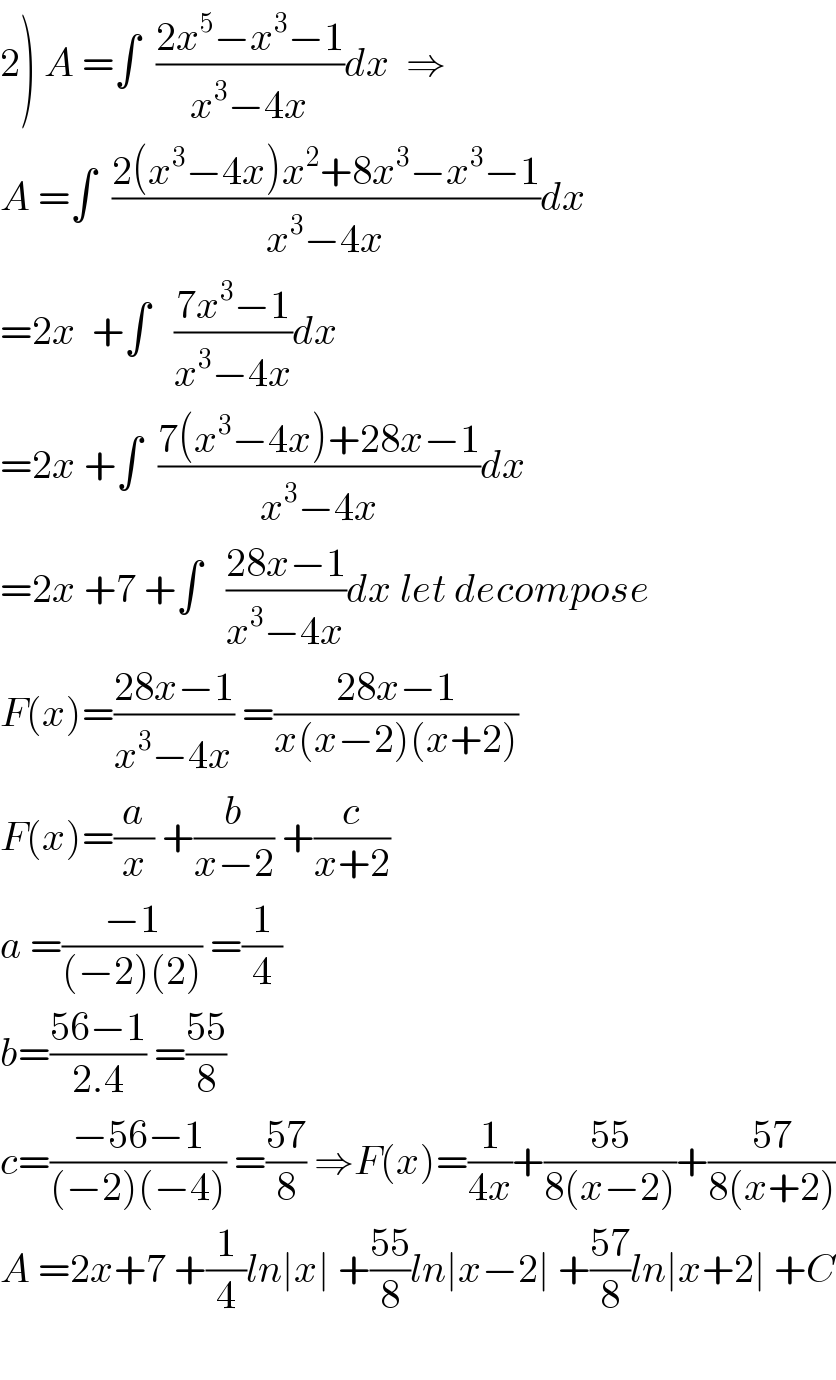
Commented by abdomathmax last updated on 25/Mar/20
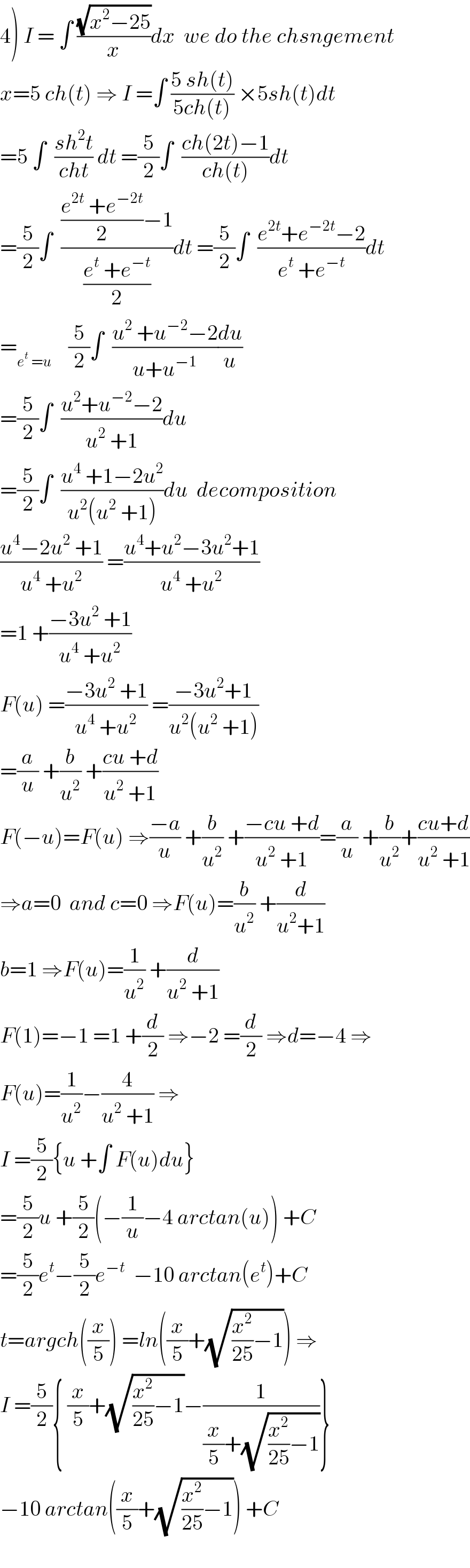
Commented by Kunal12588 last updated on 26/Mar/20
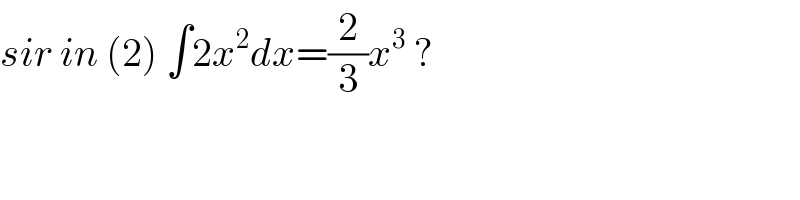
Answered by jagoll last updated on 26/Mar/20
![(3) ∫ (dx/(√(x^2 +4)))? [ x = 2 tan u ] ∫ ((2sec^2 u)/(2sec u)) du = ∫ sec u du = ln ∣sec u + tan u ∣ + c = ln ∣ ((x+(√(x^2 +4)))/2) ∣ + c](Q85916.png)
Commented by Kunal12588 last updated on 26/Mar/20
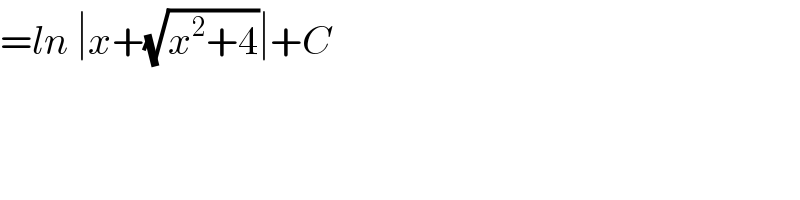
Commented by john santu last updated on 26/Mar/20
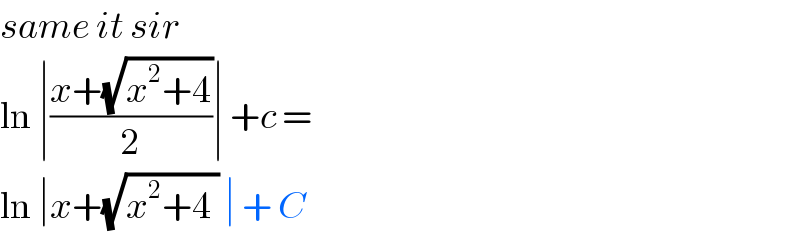
Answered by Kunal12588 last updated on 26/Mar/20
![(5)I=∫(dx/(√(5−4x−2x^2 ))) =(1/(√2))∫(dx/(√(−(x^2 +2x−(5/2))))) =(1/(√2))∫(dx/(√(−[(x+1)^2 −(7/2)]))) =(1/(√2))∫(dx/(√((7/2)−(x+1)^2 ))) =(1/(√2))sin^(−1) (((x+1)/((√7)/(√2))))+C =(1/(√2))sin^(−1) ((((√2)x+(√2))/(√7)))+C](Q85926.png)
