
Question and Answers Forum
Question Number 87105 by Chi Mes Try last updated on 02/Apr/20

Commented by mathmax by abdo last updated on 03/Apr/20
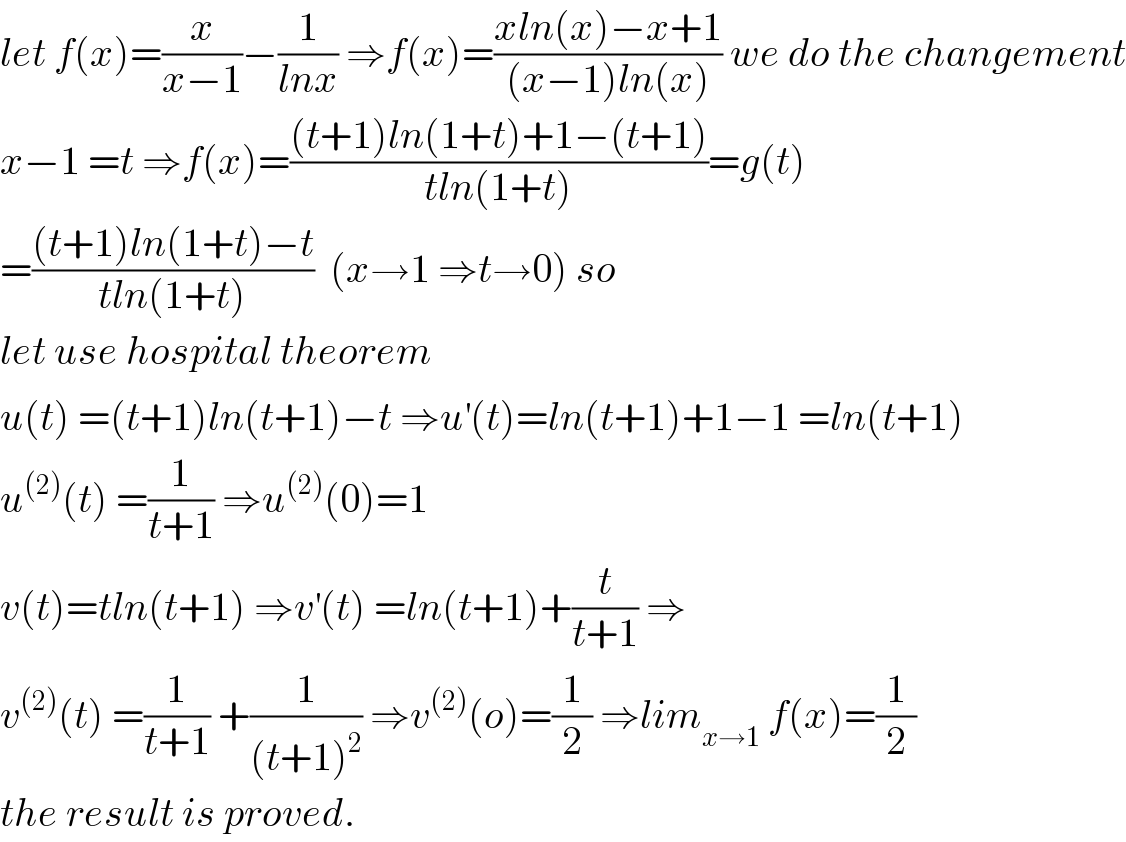
Answered by MJS last updated on 02/Apr/20
![2×l′Hopital lim_(x→1) ((xln x −x+1)/((x−1)ln x)) = lim_(x→1) (((d^2 /dx^2 )[xln x −x+1])/((d^2 /dx^2 )[(x−1)ln x])) = =lim_(x→1) (x/(x+1)) =(1/2)](Q87109.png)
Answered by $@ty@m123 last updated on 03/Apr/20
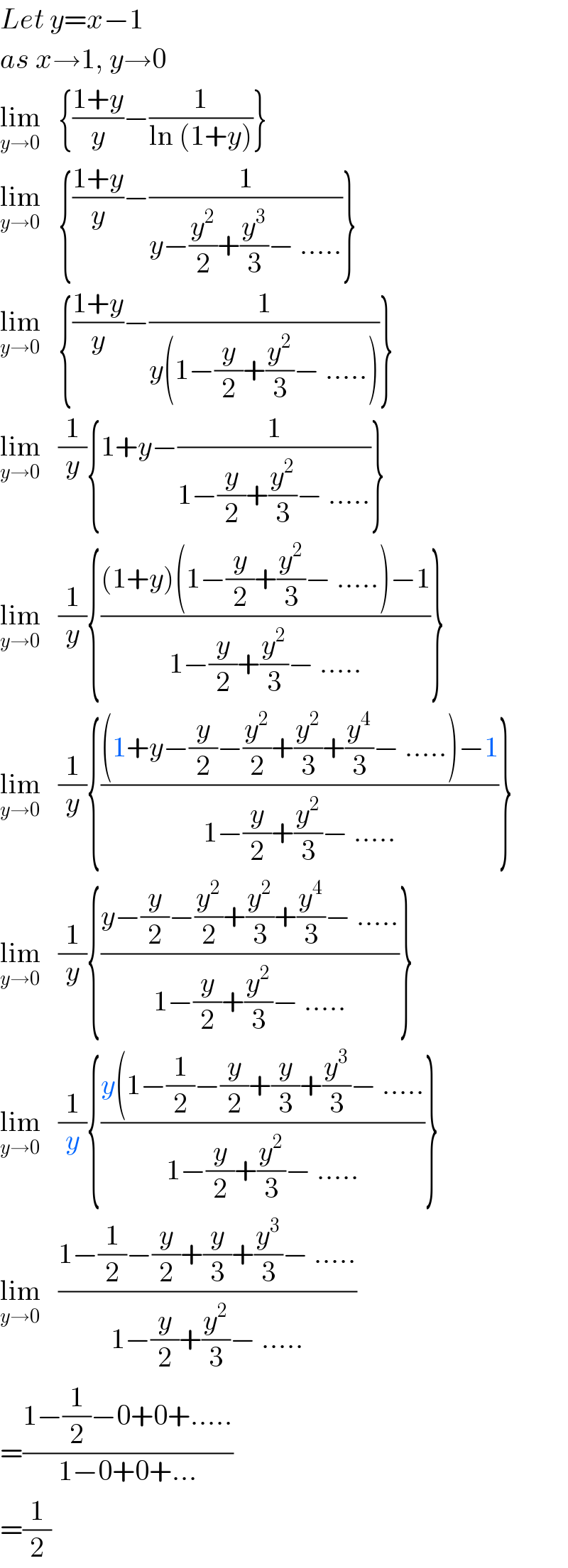
| ||
Question and Answers Forum | ||
Question Number 87105 by Chi Mes Try last updated on 02/Apr/20 | ||
 | ||
Commented by mathmax by abdo last updated on 03/Apr/20 | ||
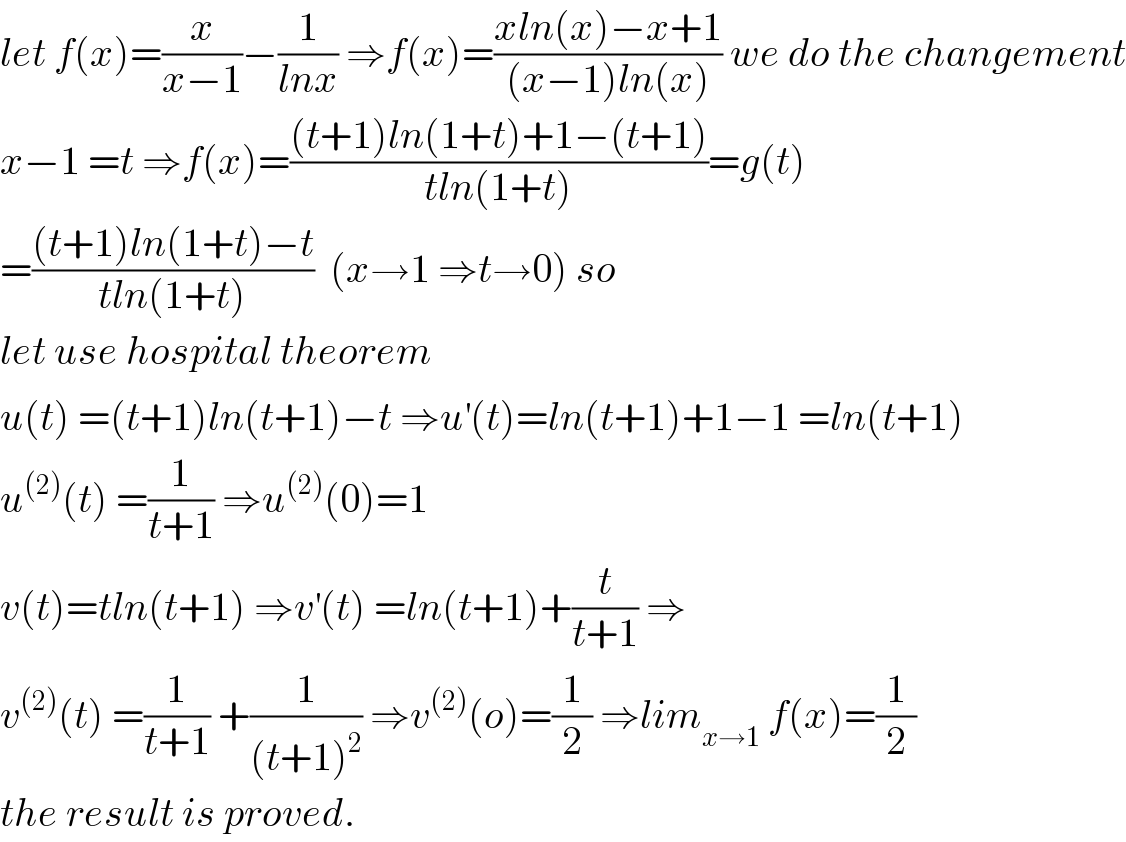 | ||
Answered by MJS last updated on 02/Apr/20 | ||
![2×l′Hopital lim_(x→1) ((xln x −x+1)/((x−1)ln x)) = lim_(x→1) (((d^2 /dx^2 )[xln x −x+1])/((d^2 /dx^2 )[(x−1)ln x])) = =lim_(x→1) (x/(x+1)) =(1/2)](Q87109.png) | ||
| ||
Answered by $@ty@m123 last updated on 03/Apr/20 | ||
 | ||
| ||