Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 87511 by M±th+et£s last updated on 04/Apr/20

Answered by TANMAY PANACEA. last updated on 04/Apr/20

$$t=x^3\to \frac{dt}{3}=x^{2}dx$$$${\int }_{ln3}^{ln4}\frac{1}{3}\times \frac{sint}{sint+sin(ln12-t)}dt=I$$$$using{\int }_a^{b}f\left(x\right)dx={\int }_a^{b}f(a+b-x)dx$$$$I=\frac{1}{3}{\int }_{ln3}^{ln4}\frac{sin(ln4+ln3-t)}{sin(ln4+ln3-t)+sin(ln12-ln4-ln3+t)}dt$$$$I=\frac{1}{3}{\int }_{ln3}^{ln4}\frac{sin(ln12-t)}{sin(ln12-t)+sint}dt$$$$2\mathit{I}=\frac{1}{3}{\int }_{oln3}^{ln4}dt$$$$I=\frac{1}{6}ln\left(\frac{4}{3}\right)$$$$$$

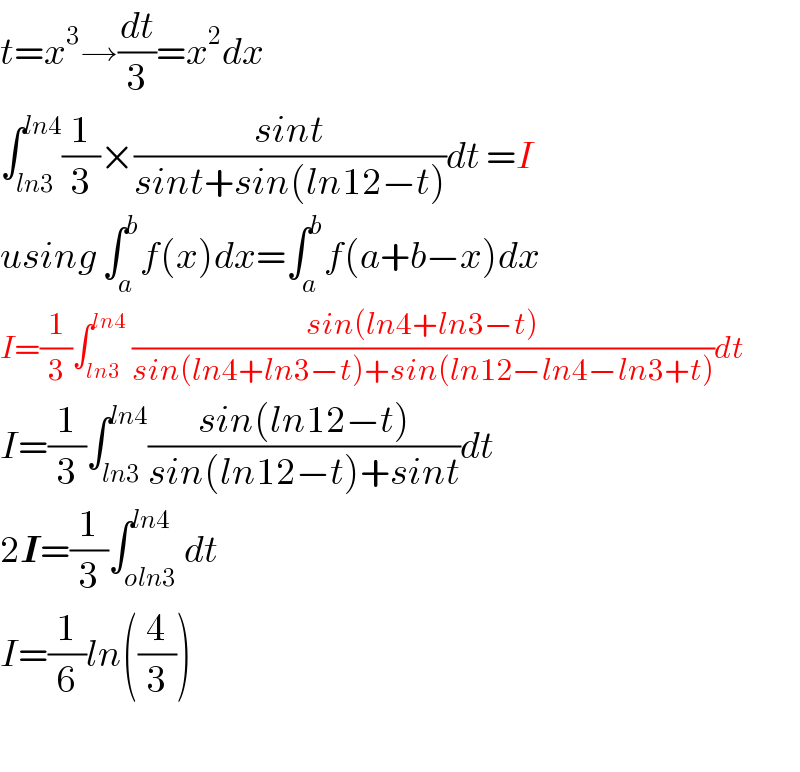
Commented by M±th+et£s last updated on 04/Apr/20

$$godblessyousir$$

Commented by TANMAY PANACEA. last updated on 04/Apr/20

$$thankyousir$$

Answered by redmiiuser last updated on 05/Apr/20

$$\sin x^3+\sin (\log 12-x^3)$$$$=2\sin \left(\frac{\log 12}{2}\right).\cos (x^3-\frac{\log 12}{2})$$$$x^3-\frac{\log 12}{2}=t$$$$dt=3x^2.dx$$$$\frac{dt}{3}=x^2.dx$$$$\sin x^3=\sin (t+\frac{\log 12}{2})$$$$\frac{1}{3.2\sin \left(\frac{\log 12}{2}\right)}{\int }_{\log 3-\frac{\log 12}{2}}^{\log 4-\frac{\log 12}{2}}\frac{\sin (t+\frac{\log 12}{2})}{\cos t}.dt$$$$=\frac{1}{6\sin \left(\frac{\log 12}{2}\right)}[\cos \left(\frac{\log 12}{2}\right).{\int }_{\log 3-\frac{\log 12}{2}}^{log4-\frac{\log 12}{2}}\tan t.dt+\sin \left(\frac{\log 12}{2}\right){\int }_{\log 3-\frac{\log 12}{2}}^{\log 4-\frac{\log 12}{2}}dt]$$$$=\frac{\cot \left(\frac{\log 12}{2}\right)}{6}.{[\log \mid sec\left(t\right)\mid ]}_{\log 3-\frac{\log 12}{2}}^{\log 4-\frac{\log 12}{2}}+\frac{1}{6}{\left[t\right]}_{\log 3-\frac{\log 12}{2}}^{\log 4-\frac{\log 12}{2}}$$$$$$$$$$$$$$

Commented by redmiiuser last updated on 05/Apr/20

$$Ihopenowyoucaninsert$$$$theborders.$$

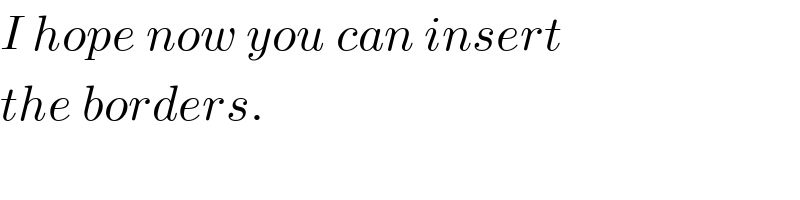
Commented by M±th+et£s last updated on 05/Apr/20

$$thankyousir$$

Commented by redmiiuser last updated on 05/Apr/20

$$welcome$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com