
Question and Answers Forum
Question Number 87540 by Power last updated on 04/Apr/20

Commented by abdomathmax last updated on 05/Apr/20
![let I =∫_0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) changement x =sh(t) give I =∫_0 ^∞ ((ch(t) dt)/((sh(t)+cht)^2 )) =∫_0 ^∞ ((ch(t))/e^(2t) )dt =∫_0 ^∞ e^(−2t) (((e^t +e^(−t) )/2))dt =(1/2)∫_0 ^∞ e^(−t) dt +(1/2)∫_0 ^∞ e^(−3t) dt =(1/2)[−e^(−t) ]_0 ^(+∞) +(1/2)[−(1/3)e^(−3t) ]_0 ^(+∞) =(1/2)(1) +(1/6) =(3/6)+(1/6) =(4/6) =(2/3)](Q87549.png)
Answered by MJS last updated on 04/Apr/20
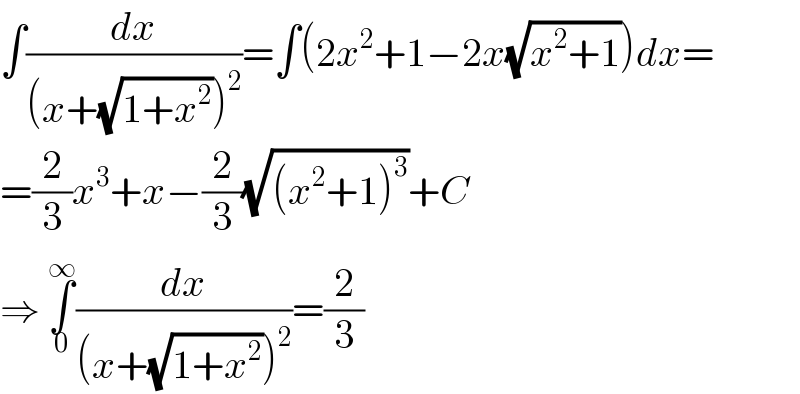
Commented by Power last updated on 05/Apr/20
| ||
Question and Answers Forum | ||
Question Number 87540 by Power last updated on 04/Apr/20 | ||
 | ||
Commented by abdomathmax last updated on 05/Apr/20 | ||
![let I =∫_0 ^∞ (dx/((x+(√(1+x^2 )))^2 )) changement x =sh(t) give I =∫_0 ^∞ ((ch(t) dt)/((sh(t)+cht)^2 )) =∫_0 ^∞ ((ch(t))/e^(2t) )dt =∫_0 ^∞ e^(−2t) (((e^t +e^(−t) )/2))dt =(1/2)∫_0 ^∞ e^(−t) dt +(1/2)∫_0 ^∞ e^(−3t) dt =(1/2)[−e^(−t) ]_0 ^(+∞) +(1/2)[−(1/3)e^(−3t) ]_0 ^(+∞) =(1/2)(1) +(1/6) =(3/6)+(1/6) =(4/6) =(2/3)](Q87549.png) | ||
Answered by MJS last updated on 04/Apr/20 | ||
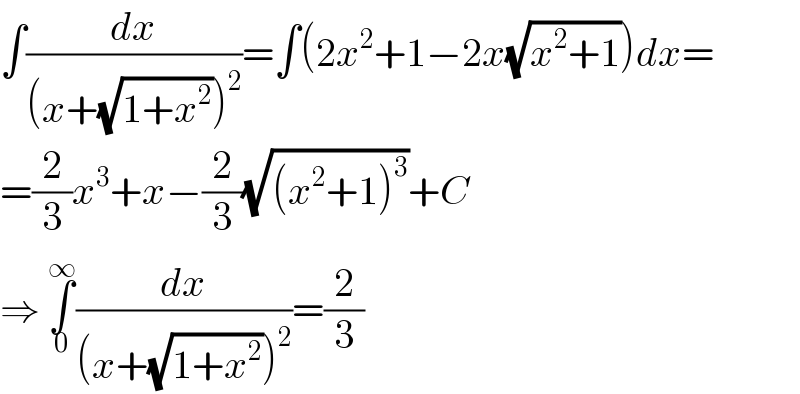 | ||
| ||
Commented by Power last updated on 05/Apr/20 | ||
 | ||