Math Question and Answers


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 88069 by Power last updated on 08/Apr/20

Commented by Power last updated on 08/Apr/20

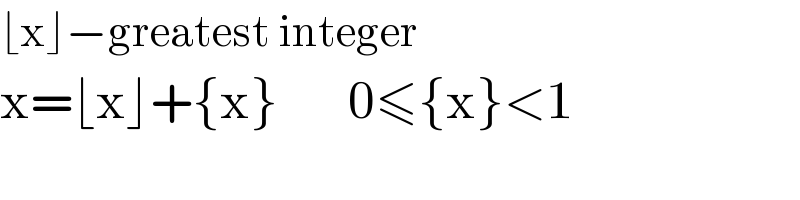
$⌊ x ⌋ - greatest integer$ $x = ⌊ x ⌋ + {x} 0 ⩽ {x} < 1$
Commented by mathmax by abdo last updated on 08/Apr/20
$A =∫_0 ^1 x{(1/x)}[(1/x)]dx we have (1/x)=[(1/x)]+{(1/x)} ⇒ A =∫_0 ^1 x((1/x)−[(1/x)])[(1/x)]dx =∫_0 ^1 (1−x[(1/x)])[(1/x)]dx we do the changement (1/x) =t ⇒ A =−∫_1 ^(+∞) (1−(1/t)[t])[t] (−(dt/t^2 )) =∫_1 ^(+∞) ((1/t^2 )−(([t]^2 )/t^3 ))dt =∫_1 ^(+∞ ) (dt/t^2 )−∫_1 ^(+∞) (([t]^2 )/t^3 )dt but we have ∫_1 ^(+∞) (dt/t^2 ) =[−(1/t)]_1 ^(+∞) =1 ∫_1 ^(+∞) (([t]^2 )/t^3 )dt =Σ_(n=1) ^∞ ∫_n ^(n+1) (n^2 /t^3 )dt =Σ_(n=1) ^∞ n^2 ∫_n ^(n+1) t^(−3) dt =Σ_(n=1) ^∞ n^2 [−(1/2)t^(−2) ]_n ^(n+1) =−(1/2)Σ_(n=1) ^∞ n^2 {(1/((n+1)^2 ))−(1/n^2 )} =−(1/2)Σ_(n=1) ^∞ ((n^2 /((n+1)^2 ))−1) =−(1/2)Σ_(n=1) ^∞ (((n^2 −(n^2 +2n+1))/((n+1)^2 ))) =−(1/2) Σ_(n=1) ^∞ ((−2n−1)/((n+1)^2 )) =Σ_(n=1) ^∞ ((2n+1)/(2(n+1)^2 )) and this serie is divergente because ((2n+1)/(2(n+1)^2 )) ∼(1/n)( n∼+∞)$
$A = \int_{0}^{1} x {\frac{1}{x}} [\frac{1}{x}] d x w e h a v e \frac{1}{x} = [\frac{1}{x}] + {\frac{1}{x}} \Rightarrow$ $A = \int_{0}^{1} x (\frac{1}{x} - [\frac{1}{x}]) [\frac{1}{x}] d x = \int_{0}^{1} (1 - x [\frac{1}{x}]) [\frac{1}{x}] d x w e d o t h e c h a n g e m e n t$ $\frac{1}{x} = t \Rightarrow A = - \int_{1}^{+ \infty} (1 - \frac{1}{t} [t]) [t] (- \frac{d t}{t^{2}})$ $= \int_{1}^{+ \infty} (\frac{1}{t^{2}} - \frac{{[t]}^{2}}{t^{3}}) d t = \int_{1}^{+ \infty} \frac{d t}{t^{2}} - \int_{1}^{+ \infty} \frac{{[t]}^{2}}{t^{3}} d t b u t w e h a v e$ $\int_{1}^{+ \infty} \frac{d t}{t^{2}} = {[- \frac{1}{t}]}_{1}^{+ \infty} = 1$ $\int_{1}^{+ \infty} \frac{{[t]}^{2}}{t^{3}} d t = \sum_{n = 1}^{\infty} \int_{n}^{n + 1} \frac{n^{2}}{t^{3}} d t = \sum_{n = 1}^{\infty} n^{2} \int_{n}^{n + 1} t^{- 3} d t$ $= \sum_{n = 1}^{\infty} n^{2} {[- \frac{1}{2} t^{- 2}]}_{n}^{n + 1} = - \frac{1}{2} \sum_{n = 1}^{\infty} n^{2} {\frac{1}{{(n + 1)}^{2}} - \frac{1}{n^{2}}}$ $= - \frac{1}{2} \sum_{n = 1}^{\infty} (\frac{n^{2}}{{(n + 1)}^{2}} - 1) = - \frac{1}{2} \sum_{n = 1}^{\infty} (\frac{n^{2} - (n^{2} + 2 n + 1)}{{(n + 1)}^{2}})$ $= - \frac{1}{2} \sum_{n = 1}^{\infty} \frac{- 2 n - 1}{{(n + 1)}^{2}} = \sum_{n = 1}^{\infty} \frac{2 n + 1}{2 {(n + 1)}^{2}} a n d t h i s s e r i e i s d i v e r g e n t e$ $b e c a u s e \frac{2 n + 1}{2 {(n + 1)}^{2}} \sim \frac{1}{n} (n \sim + \infty)$
	Answered by mahdi last updated on 08/Apr/20
	$(1/x)=[(1/x)]+{(1/x)}⇒x{(1/x)}[(1/x)]=x((1/x)−[(1/x)])[(1/x)] =[(1/x)]−x[(1/x)]^2 ∫_0 ^1 x{(1/x)}[(1/x)]dx=∫_0 ^1 ([(1/x)]−x[(1/x)]^2 )dx= Σ_(n=1) ^∞ ∫_(1/(n+1)) ^(1/n) ([(1/x)]−x[(1/x)]^2 )dx= Σ_(n=1) ^∞ ∫_(1/(n+1)) ^(1/n) (n−xn^2 )dx=Σ_(n=1) ^∞ [nx−((x^2 n^2 )/2)]_(1/(n+1)) ^(1/n) Σ_(n=1) ^∞ ((1/(n+1))−(1/(2(n+1)^2 )))=Σ_(n=1) ^∞ (((2n+1)/(2(n+1)^2 )))$
	$\frac{1}{x} = [\frac{1}{x}] + {\frac{1}{x}} \Rightarrow x {\frac{1}{x}} [\frac{1}{x}] = x (\frac{1}{x} - [\frac{1}{x}]) [\frac{1}{x}]$ $= [\frac{1}{x}] - x {[\frac{1}{x}]}^{2}$ $\int_{0}^{1} x {\frac{1}{x}} [\frac{1}{x}] dx = \int_{0}^{1} ([\frac{1}{x}] - x {[\frac{1}{x}]}^{2}) dx =$ $\underset{n = 1}{\sum^{\infty}} \int_{\frac{1}{n + 1}}^{\frac{1}{n}} ([\frac{1}{x}] - x {[\frac{1}{x}]}^{2}) dx =$ $\underset{n = 1}{\sum^{\infty}} \int_{\frac{1}{n + 1}}^{\frac{1}{n}} (n - {xn}^{2}) dx = \underset{n = 1}{\sum^{\infty}} {[nx - \frac{x^{2} n^{2}}{2}]}_{\frac{1}{n + 1}}^{\frac{1}{n}}$ $\underset{n = 1}{\sum^{\infty}} (\frac{1}{n + 1} - \frac{1}{2 {(n + 1)}^{2}}) = \underset{n = 1}{\sum^{\infty}} (\frac{2 n + 1}{2 {(n + 1)}^{2}})$
	Commented by mahdi last updated on 08/Apr/20

	$i think : \underset{n = 1}{\sum^{\infty}} (\frac{2 n + 1}{2 {(n + 1)}^{2}}) = + \infty$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum