
Question and Answers Forum
Question Number 89244 by 174 last updated on 16/Apr/20
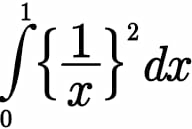
Commented by mathmax by abdo last updated on 16/Apr/20
![A =∫_0 ^1 {(1/x)}^2 dx cha7gement (1/x)=t give A =−∫_1 ^(+∞) {t}^2 (−(dt/t^2 )) =∫_1 ^(+∞) (((t−[t])^2 )/t^2 )dt = ∫_1 ^(+∞) ((t^2 −2t[t]+[t]^2 )/t^2 )dt =∫_1 ^(+∞) (1−2(([t])/t) +(([t]^2 )/t^2 ))dt =Σ_(n=1) ^∞ ∫_n ^(n+1) (1−2(n/t) +(n^2 /t^2 ))dt but ∫_n ^(n+1) (1−2(n/t)+(n^2 /t^2 ))dt =[t−2nln(t)−(n^2 /t)]_n ^(n+1) =1 −2nln(((n+1)/n))−n^2 ((1/(n+1))−(1/n)) =1−2nln(1+(1/n))+(n^2 /(n(n+1))) =1−2nln(1+(1/n))+(n/(n+1)) ln(1+(1/n))∼−2n((1/n)−(1/(2n^2 )))=−2+(1/n^2 ) ⇒ 1−2nln(1+(1/n))+(n/(n+1)) ∼(1/n^2 ) and Σ (1/n^2 ) is convergent....](Q89277.png)
| ||
Question and Answers Forum | ||
Question Number 89244 by 174 last updated on 16/Apr/20 | ||
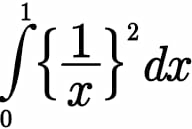 | ||
Commented by mathmax by abdo last updated on 16/Apr/20 | ||
![A =∫_0 ^1 {(1/x)}^2 dx cha7gement (1/x)=t give A =−∫_1 ^(+∞) {t}^2 (−(dt/t^2 )) =∫_1 ^(+∞) (((t−[t])^2 )/t^2 )dt = ∫_1 ^(+∞) ((t^2 −2t[t]+[t]^2 )/t^2 )dt =∫_1 ^(+∞) (1−2(([t])/t) +(([t]^2 )/t^2 ))dt =Σ_(n=1) ^∞ ∫_n ^(n+1) (1−2(n/t) +(n^2 /t^2 ))dt but ∫_n ^(n+1) (1−2(n/t)+(n^2 /t^2 ))dt =[t−2nln(t)−(n^2 /t)]_n ^(n+1) =1 −2nln(((n+1)/n))−n^2 ((1/(n+1))−(1/n)) =1−2nln(1+(1/n))+(n^2 /(n(n+1))) =1−2nln(1+(1/n))+(n/(n+1)) ln(1+(1/n))∼−2n((1/n)−(1/(2n^2 )))=−2+(1/n^2 ) ⇒ 1−2nln(1+(1/n))+(n/(n+1)) ∼(1/n^2 ) and Σ (1/n^2 ) is convergent....](Q89277.png) | ||