
Question and Answers Forum
Question Number 96898 by bobhans last updated on 05/Jun/20

Commented by PRITHWISH SEN 2 last updated on 05/Jun/20
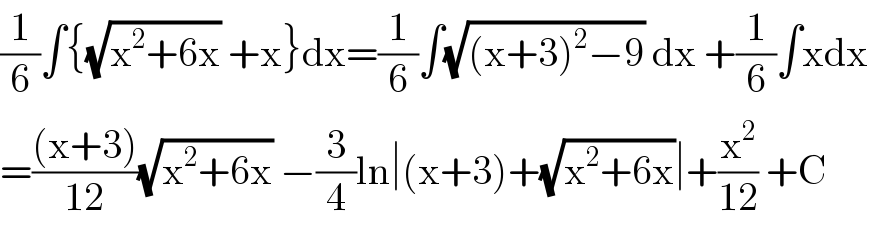
Answered by john santu last updated on 05/Jun/20
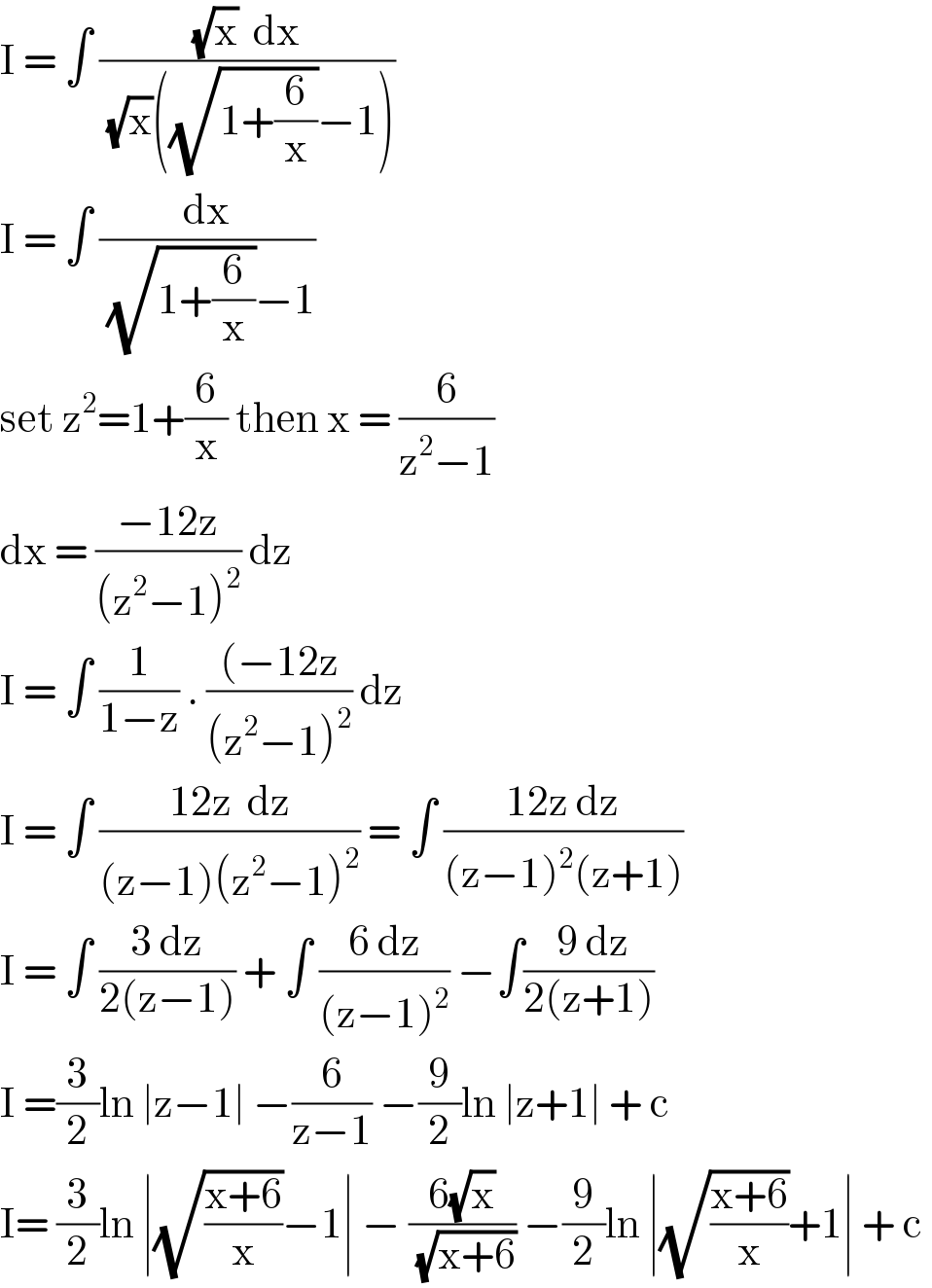
Answered by Sourav mridha last updated on 05/Jun/20
![=(1/6)[∫(√(x^2 +6x)) +(1/2)x^2 ] =(1/6)[∫(√((x+3)^2 −3^2 ))d(x+3)]+(1/(12))x^2 =(1/6)[(((x+3))/2).(√(x^2 +6x)) −(9/2)ln[(x+3)+(√(x^2 +6x))] +(1/(12))x^2 +c](Q96910.png)
| ||
Question and Answers Forum | ||
Question Number 96898 by bobhans last updated on 05/Jun/20 | ||
 | ||
Commented by PRITHWISH SEN 2 last updated on 05/Jun/20 | ||
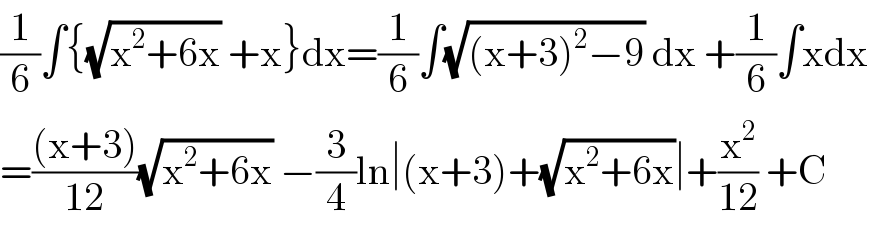 | ||
Answered by john santu last updated on 05/Jun/20 | ||
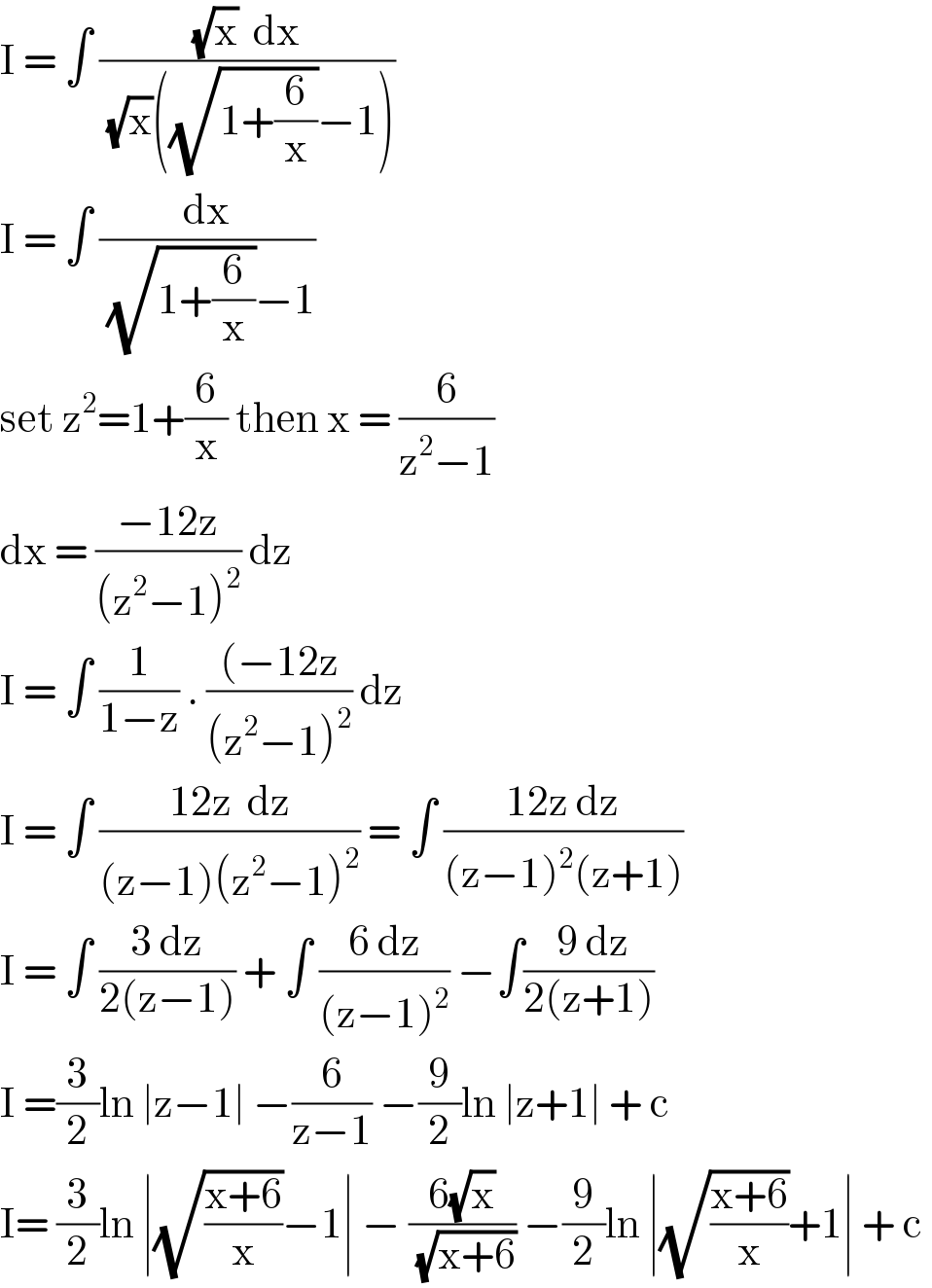 | ||
| ||
Answered by Sourav mridha last updated on 05/Jun/20 | ||
![=(1/6)[∫(√(x^2 +6x)) +(1/2)x^2 ] =(1/6)[∫(√((x+3)^2 −3^2 ))d(x+3)]+(1/(12))x^2 =(1/6)[(((x+3))/2).(√(x^2 +6x)) −(9/2)ln[(x+3)+(√(x^2 +6x))] +(1/(12))x^2 +c](Q96910.png) | ||
| ||