
Question and Answers Forum
Relation and FunctionsQuestion and Answers: Page 2




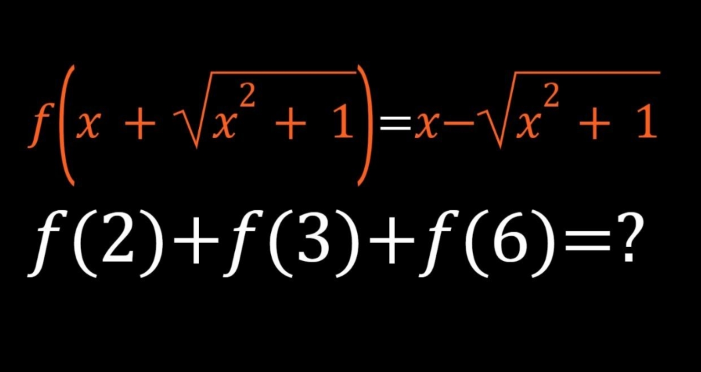
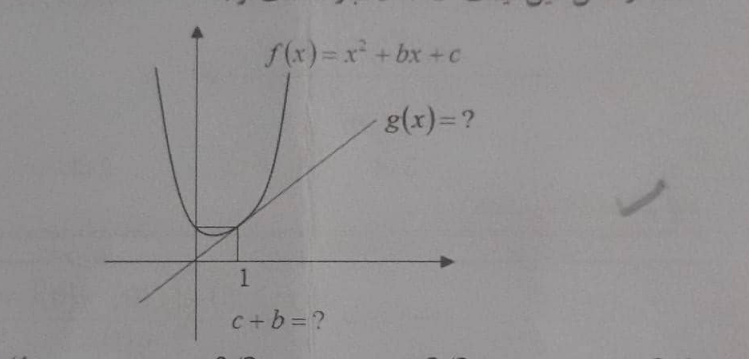
|
Question and Answers Forum |
Relation and FunctionsQuestion and Answers: Page 2 |
| soit f: R^3 →R^3 f(x,y,z)=(x+y,2x−y,x+z) •1 Ecrire la matrice M de cette application dans la base canonique B de R^3 •2 Calculer f(1,2,3)de 2 manieres differentes −en utilisant la definition de f −en utilisant la matrice M •3 determiner bsse de Ker( f) et de Im(f) •4 soient v_1 =(1,1,0) v_2 =(1,2,1) v_3 =(1,3,1) Montrer que la famille E=(v_1 , v_2 , v_3 )est une base de R^3 •5Calculer f(v_1 ) donner ses coordonnes(locus) dans bass E avec f(v_2 )=v_1 +6v_2 −4v_3 f(v_3 )=2v_1 +8v_2 −6v_3 •6 Ecrire la matrice N de f dans base F •7 Retrouver cette matrice a partir de M en utilisant la formule de changement de base |
| let a , b >0 find all differentiable function f:(0,∞)→(0,∞) such that f′((a/x)) = ((bx)/(f(x))) , ∀ x>0 |

|

|
| let ABC a given triangle. Can we find three positions I,J,K on the side AB,AC,BC Such that IJK is equilateral? |
| f(x)={1+((√x^2 )/x) if x#0 2 if x=0 study the continuty of f in 0 |
| find the seauence u_n wich verify u_0 =1 and u_n +u_(n+1) =(((−1)^n )/n) for n≥1 |
| if f(−1)=f(0)=f(2)=0 and f(1)=6 then find f(x)=? |

|
| f(x+1)−f(x)=3f(x)×f(x+1) D_f =N 2023×f(1402)=1 have equation f(x)=1 solution? |

|
| Find all polynomials P(x) with real coefficients such that for all nonzero real numbers x, P(x)+P((1/x))=((P(x+(1/x))+P(x−(1/x)))/2) |
| Give a function f: R→(0;+∞) continous on R and such that f(x+y) = f(x).f(y) a. Prove f(0) = 1 b. Let h(x) = ln[f(x)]. Prove that: h(x+y) = h(x) + h(y) c. Find all the function f such that problem request |
| f(xf(y)+x)=xy+f(x) f:R→R f(x)=? |
| 2^x +9+2^x =40 |
| 3×5^x +5^(x+1) =8×5^3 |
| Find L^(−1) { (1/(2^( s) (√( 2s+1)) )) }= ? inverse laplace transform... |
| ∫^( +∞) _( 0) (((ln(t+(√(1+t^2 ))))/t))^2 =(π^2 /2) |
| f: R→R f(f(x+y))=f(x)+f(y) Find f(x)=¿ |
| Σ_(x∈R) x = 0 and Π_(x∈R^∗ ) x = −1 |
| find f(x) if f(x+(√(x^2 +1))) = (x/(x+1)) |
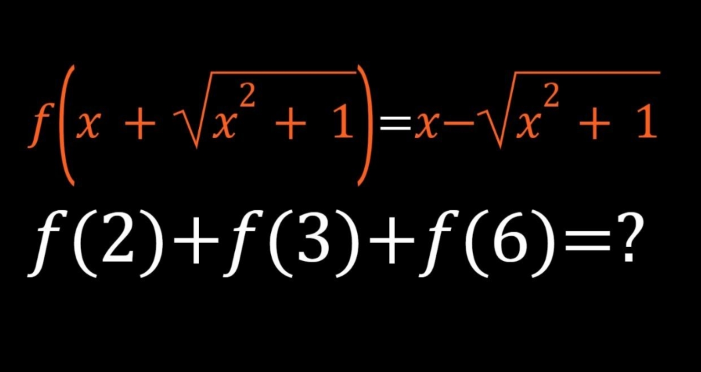
|
| Prove that ∀n∈N ∫^( n+1) _( n) lnt dt ≤ ln(∫^( n+1) _n t dt) |
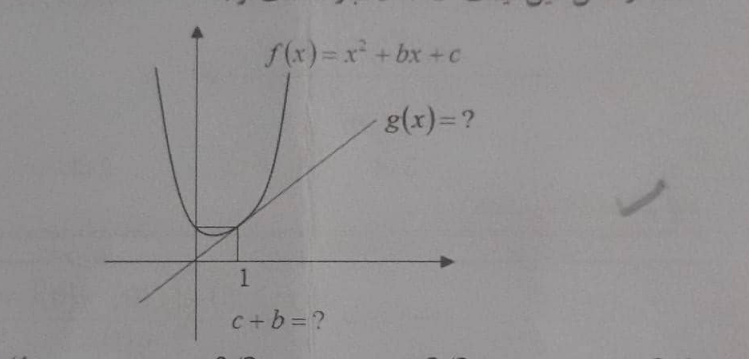
|