
Question and Answers Forum
Relation and FunctionsQuestion and Answers: Page 3




|
Question and Answers Forum |
Relation and FunctionsQuestion and Answers: Page 3 |
|
| find the domain of definition of this function for t∈]0;1[ 𝛒(x)=∫_x ^(2x) (1/(lnt))dt ptiCantor |
| f^2 (x)+2f(x)=x^2 −8x+15 f(x)=? |
| If (f(x))=x^2 −x+1 find the value of f(1971)+f(2021)+f(50) |
| if f(x) is also differentiable on R such that f′(x) > f(x) ∀ x ∈ R and f(x_0 ) = 0 then prove that f(x) ≥ 0 ∀ x > x_0 |
| find all function f: R → R such that ∀x, y∈R, f(x−f(y))=f(f(y))+xf(y)+f(x)−1. |
| (f(x))^2 −4xf(x)+3=0 f^(−1) (3)=? |
|

|
| Can this be optimized (getting the minimum) using backprobagation? α(x_i ,y_i ,h_i )=(h_i −x_i )^2 +y_i ^2 β(y_i ,h_i )=y_i h_i ^2 −2uy_i h_i γ(h_i )=h_i ^4 −4uh_i ^3 +4u^2 h_i ^2 Cost=Σ_(i=0) ^m (cα(x_i ,y_i ,h_i )−2c^2 β(y_i ,h_i )+c^3 γ(h_i )) and how? |
|
| What is the nearest point in f(x) to (5,2) where f(x)=−0.5x^2 +3 |
| Show that lim_((x,y)→(0,0)) ((x^2 −y^2 )/(x^2 +y^2 )) does not exist |
| Find the relative maximum and minimum of the function f(x,y)=x^3 +y^3 −3x−12y+20 |

|

|

|
| find f(x) 1:f(((x+1)/(x−1)))=x+3; x≠1 2:f(((2x+1)/(x−1)))=x^2 +2x ;x≠1 3:f(x+1)+f(x−y)=2f(x)cosy ∀x,y f(0)=f((π/2))=1 |
| Given f(x)=x^5 +ax^4 +bx^3 +cx^2 +dx+c and f(1)=f(2)=f(3)=f(4)=f(5). Find a. |
| find function f(x) and g(x) such that { ((f(2x−1)+g(1−x)=x+1)),((f((x/(x+1)))+2g((1/(2x+2)))=3)) :} |
| Given f(x)+2f((1/x))+3f((x/(x−1)))=x f(x)=? |
| Let R denote a set of all ordered pairs (x, y) of integers such that x−y is an integral multiple of 3. Which of the followings ordered pairs belong to R (9,3) (3, 9),( 1 ,2) (1, 5),(7, 2) (0, 4), (4 ,7). (note: a is an integral multiple of b if a=kb where k is an integer) |
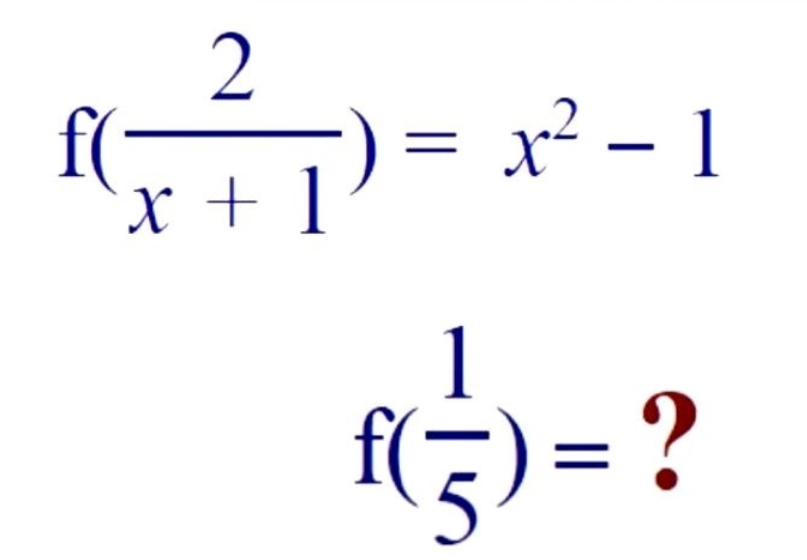
|
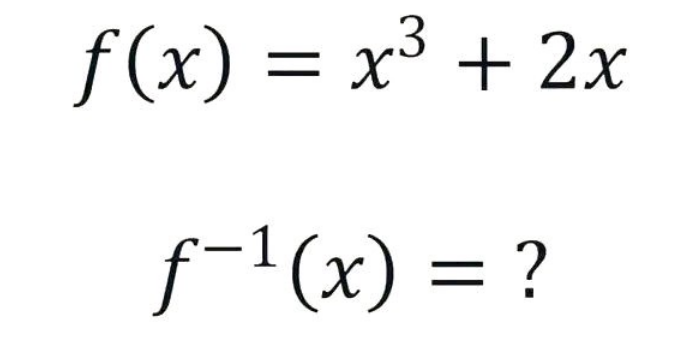
|
| Σ_(r=1) ^n 3^(r−1) sin^3 ((θ/3^r )) = ? |