
Question and Answers Forum
Relation and FunctionsQuestion and Answers: Page 4





|
Question and Answers Forum |
Relation and FunctionsQuestion and Answers: Page 4 |
|
| solve: W(In(4x))=(√((x−1))) |
| Given f(x)= (([(1/3)x]∣2x∣+Ax)/(∣4−x^2 ∣)) if f ′(−1)= 5 then A=? [ ] = floor function |

|
| ∫_1 ^( n) ((⌊x⌋)/x^2 )dx = |
| solution set of log_x^(2 ) ((x/(∣x∣))−x)≥0 |
| let f:[0,1]→ R be given by f(x) = (((1+x^(1/3) )^3 +(1−x^(1/3) )^3 )/(8(1+x))) then max{f(x): x∈[0,1]}−min{f(x):x∈[0,1]} is |
| • D={z : ∣z∣<1} • H (A→B) denotes the set of holomorfic functions from A to B • We define: W={f∈H (D→R) : ∣∣f∣∣_W <∞ } where ∣∣ ∙ ∣∣_W : { (W,→,R_+ ),(f, ,(Σ_(n=0) ^∞ ((∣f^((n)) (0)∣)/(n!)))) :} Let f∈W Show that ∀g∈H ( f(D^ )), g○f∈W tip: show that ∣∣h∣∣_W ≤cste × Sup_(z∈D) {∣h(z)∣+∣h′′(z)∣} and that W is an algebra then, re−wright f=f_1 +f_2 with f_2 : z Σ_(n=N) ^∞ ((f^((n)) (0))/(n!))z^n with N great enough to make sure that Σ_(n=0) ^∞ ((g^((n)) (0))/(n!))f_2 ^( n) is well defined and converges over W. ∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙ |

|
| f(x)=f(x−1)+x^2 +2x f(6)=33 faind volue of f(50)=? |
| find the range of x+y such that (x−2)^2 + (y−4)^2 = 49 |
| in AB_ ^Δ C : ((b−c)/(h_a )) =k , and A^ is given. B^ , C^ =? |
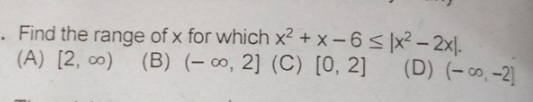
|
| solve the follwing equation x(√(x )) + y(√(y )) = 3 and x(√(y )) + y(√(x )) = 2 someone solve the above equations in the following way x^3 + y^3 + 2xy(√(xy )) = 9.....(1) and x^2 y + y^2 x + 2xy(√(xy )) = 4......(2) (1) − (2) ⇒ (x − y)(x^2 − y^2 ) = 5 hence x = 3 and y = 2 which is obiviusly does not satisfy the original equations. where is the fallacy in the above solution? Please explain. |
| find the range of the function f(x) = cosx{sinx + (√(sin^2 x + sin^2 α )) } |
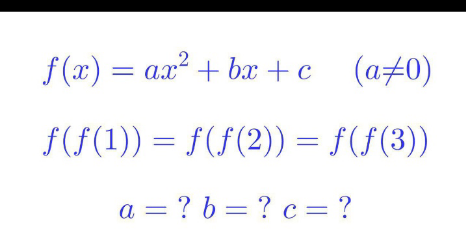
|

|

|
| solve for all x ⌊x^2 ⌋ − ⌊x⌋^2 = 100 |
| let u_n = ∫_0 ^1 x^n artan(nx)dx 1)lim u_n ? 2)nature of Σ u_n 3) calculate u_n 4)equivalent of u_n ? |
| { ((f((x/(x^2 +1)))=(x^2 /(x^4 +2x^2 +1)))),((f((√3) )=?)) :} |
| f(x)=(x+1)(x+2)....(x+n) 1)calculate f^′ (x) (n≥1) 2)decompose F=(1/f) |
| find ∫(√(x+(√(1−x))))dx |
| if f(x) is 2^(nd) digre function f(x−1)+f(x)+f(x+1)=x^2 +1 then faind f(2)=? |
| U_n = ((((−4)^(n+1) −1)/(1−(−4)^n )))U_(n−1) with U_0 =1 find U_(n ) in terms of n |

|