Question and Answers Forum
Question Number 157489 by MathSh last updated on 23/Oct/21
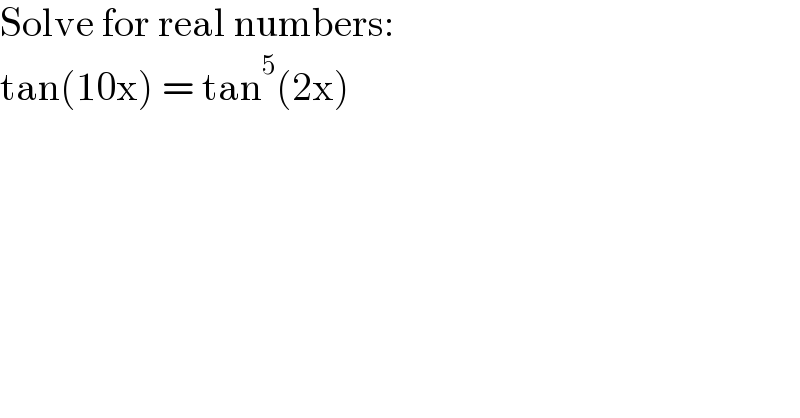
Answered by MJS_new last updated on 24/Oct/21
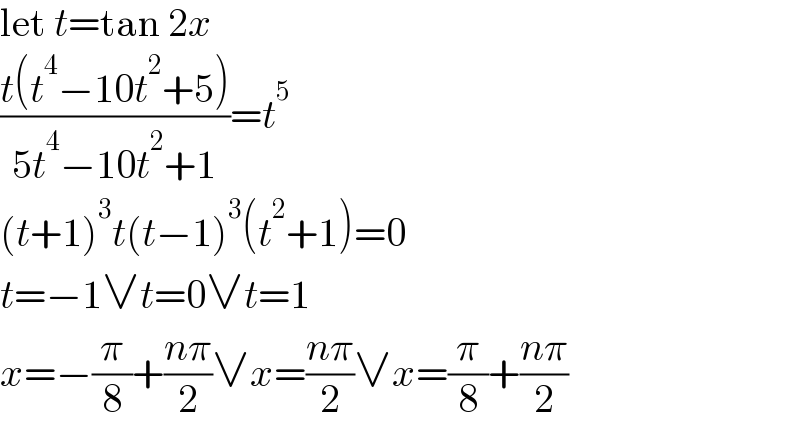
Commented by tounghoungko last updated on 24/Oct/21
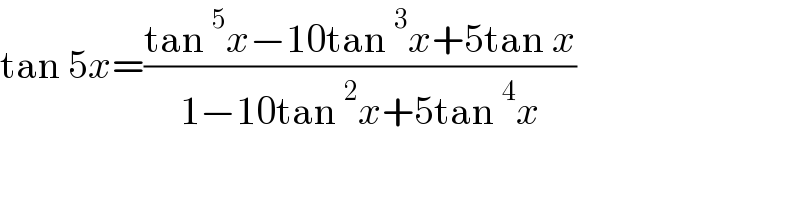
Commented by MJS_new last updated on 24/Oct/21

Commented by MathSh last updated on 24/Oct/21
Answered by tounghoungko last updated on 24/Oct/21
![Solve for x∈R . tan (10x)=tan^5 (2x) ⇔ tan (5θ)=((sin^5 θ)/(cos^5 θ)) ,[θ=2x] ⇔((sin 5θ)/(cos 5θ)) = ((sin^5 θ)/(cos^5 θ)) ⇔ ((5sin θ−20sin^3 θ+16sin^5 θ)/(5cos θ−20cos^3 θ+16cos^5 θ))=((sin^5 θ)/(cos^5 θ)) ⇔5sin θcos^5 θ−20sin^3 θcos^5 θ+16sin^5 θcos^5 θ= 5cos θsin^5 θ−20cos^3 θsin^5 θ+16cos^5 θsin^5 θ ⇔sin θcos θ [5cos^4 θ−20sin^2 θcos^4 θ+16sin^4 θcos^4 θ− [5sin^4 θ+20cos^2 θsin^4 θ−16sin^4 θcos^4 θ ]=0 ⇔ (1/2)sin 2θ [5(cos^4 θ−sin^4 θ)+20(cos^2 θsin^4 θ−sin^2 θcos^4 θ)]=0 ⇔(1/2)sin 2θ [5(cos^2 θ−sin^2 θ)+20cos^2 θsin^2 θ(sin^2 θ−cos^2 θ)]=0 ⇔(5/2)sin 2θ cos 2θ (1−sin^2 2θ)=0 ⇔(5/4)sin 4θ (1−sin^2 2θ)=0 (i) (5/4)sin 4θ=0⇒ { ((4θ=2nπ)),((4θ=(1+2n)π)) :} ⇒ { ((8x=2nπ)),((8x=(1+2n)π)) :}⇒ { ((x=((nπ)/4))),((x=(((1+2n)/8))π)) :} (ii) 1−sin^2 2θ=0 ⇒ { ((sin 2θ=1)),((sin 2θ=−1)) :} ⇒ { (( 2θ=(π/2)+2kπ)),((2θ=((3π)/2)+2kπ)) :} { ((4x=(π/2)+2kπ)),((4x=((3π)/2)+2kπ)) :}⇒ { ((x=(((4k+1)/8))π)),((x=(((3+4k)/8))π)) :}](Q157532.png)
Commented by MathSh last updated on 24/Oct/21