Solve in real numbers the system of equations { (((3x+y)(x+3y)(√(xy)) =14)),(((x+y)(x^2 +14xy+y^2 )= 36)) :}


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 119795 by bobhans last updated on 27/Oct/20
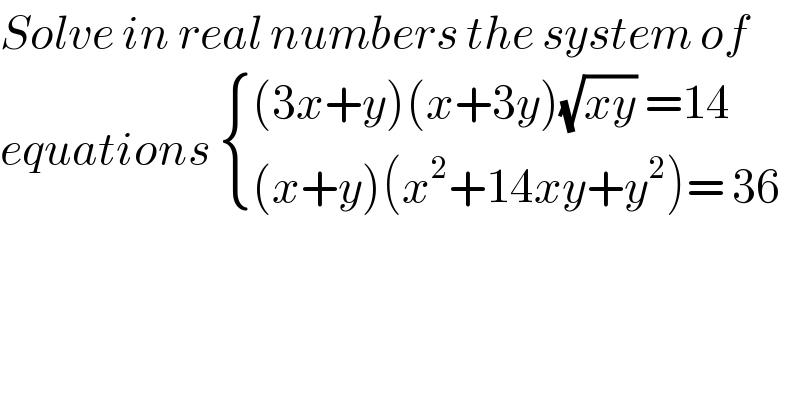
$Solve in real numbers the system of equations { (((3x+y)(x+3y)(√(xy)) =14)),(((x+y)(x^2 +14xy+y^2 )= 36)) :}$
$S o l v e i n r e a l n u m b e r s t h e s y s t e m o f$ $e q u a t i o n s {\begin{cases} (3 x + y) (x + 3 y) \sqrt{x y} = 14 \\ (x + y) (x^{2} + 14 x y + y^{2}) = 36 \end{cases}$
	Answered by 1549442205PVT last updated on 27/Oct/20
	$Put x=ky we get (((3k+1)(k+3)(√k) )/((k+1)(k^2 +14k+1)))=(7/(18)) ⇔18(3k+1)(k+3)(√k) =7(k+1)(k^2 +14k+1) { (((3x+y)(x+3y)(√(xy)) =14 (1))),(((x+y)(x^2 +14xy+y^2 )= 36 (2))) :} (2)⇔x^4 +15x^2 y+15xy^2 +y^3 −36=0(3) ⇔324k(3k^2 +10k+3)^2 =49(k^3 +15k^2 +15k+1)^2 ⇔324k(9k^4 +118k^2 +60k^3 +60k+9) =49(k^6 +30k^5 +255k^4 +452k^3 +255k^2 +30k+1) ⇔49k^6 −1446k^5 −6945k^4 −16084k^3 −6945k^2 −1446k+49i ⇔49(k^3 +(1/k^3 ))−1446(k^2 +(1/k^2 ))−6945(k+(1/k))−16084=0(∗) Put k+(1/k)=t⇒k^2 +(1/k^2 )=t^2 −2 k^3 +(1/k^3 )=t^3 −3t.Replace into we get 49(t^3 −3t)−1446(t^2 −2)−6945t−16084=0 ⇔49t^3 −1446t^2 −7092t−13192=0 49(t−34)(49t^2 +220t+338)=0 ⇒t=34⇔k+(1/k)=34⇔k^2 −34k+1=0 Δ′=17^2 −1=288=12^2 .2 k=17±12(√2) i)k=17+12(√2) ⇒x=(17+12(√2))y Replace into (3)we get (3)⇔37/y^3 =(k^3 +15k^2 +15k+1) =k(k^2 +1)+15(k^2 +1)+14k−14 =k(34k)+15.34k+14k−14 =34(k^2 +1)+524k−48=34.34k+524k−48 =1680k−48=1680(17+12(√2))−48=36/y^3 ⇔28512+20160(√2)=36/y^3 y^3 =((36)/(28512+20160(√2))) ⇒y=^3 (√(1/(792+560(√2)))) =^3 (√(1/((6+4(√2))^3 )))=(1/(6+4(√2)))=((3−2(√2))/2) x=(17+12(√2)).((3−2(√2))/2)=((3+2(√2))/2) ii)k=17−12(√2) .Similarly,we get y=((3+2(√2))/2),x=((3−2(√2))/2) Thus the given system has two solutions (x,y)∈{(((3−2(√2))/2),((3+2(√2))/2)),(((3+2(√2))/2),((3−2(√2))/2))}$
	$Put x = ky we get$ $\frac{(3 k + 1) (k + 3) \sqrt{k}}{(k + 1) (k^{2} + 14 k + 1)} = \frac{7}{18}$ $\Leftrightarrow 18 (3 k + 1) (k + 3) \sqrt{k} = 7 (k + 1) (k^{2} + 14 k + 1)$ ${\begin{cases} (3 x + y) (x + 3 y) \sqrt{x y} = 14 (1) \\ (x + y) (x^{2} + 14 x y + y^{2}) = 36 (2) \end{cases}$ $(2) \Leftrightarrow x^{4} + {15 x}^{2} y + {15 xy}^{2} + y^{3} - 36 = 0 (3)$ $\Leftrightarrow 324 k {({3 k}^{2} + 10 k + 3)}^{2} = 49 {(k^{3} + {15 k}^{2} + 15 k + 1)}^{2}$ $\Leftrightarrow 324 k ({9 k}^{4} + {118 k}^{2} + {60 k}^{3} + 60 k + 9)$ $= 49 (k^{6} + {30 k}^{5} + {255 k}^{4} + {452 k}^{3} + {255 k}^{2} + 30 k + 1)$ $\Leftrightarrow {49 k}^{6} - {1446 k}^{5} - {6945 k}^{4} - {16084 k}^{3} - {6945 k}^{2} - 1446 k + 49 i$ $\Leftrightarrow 49 (k^{3} + \frac{1}{k^{3}}) - 1446 (k^{2} + \frac{1}{k^{2}}) - 6945 (k + \frac{1}{k}) - 16084 = 0 (*)$ $Put k + \frac{1}{k} = t \Rightarrow k^{2} + \frac{1}{k^{2}} = t^{2} - 2$ $k^{3} + \frac{1}{k^{3}} = t^{3} - 3 t . Replace into we get$ $49 (t^{3} - 3 t) - 1446 (t^{2} - 2) - 6945 t - 16084 = 0$ $\Leftrightarrow {49 t}^{3} - {1446 t}^{2} - 7092 t - 13192 = 0$ $49 (t - 34) ({49 t}^{2} + 220 t + 338) = 0$ $\Rightarrow t = 34 \Leftrightarrow k + \frac{1}{k} = 34 \Leftrightarrow k^{2} - 34 k + 1 = 0$ $Δ^{'} = 17^{2} - 1 = 288 = 12^{2} . 2$ $k = 17 \pm 12 \sqrt{2}$ $i) k = 17 + 12 \sqrt{2} \Rightarrow x = (17 + 12 \sqrt{2}) y$ $Replace into (3) we get$ $(3) \Leftrightarrow 37 / y^{3} = (k^{3} + {15 k}^{2} + 15 k + 1)$ $= k (k^{2} + 1) + 15 (k^{2} + 1) + 14 k - 14$ $= k (34 k) + 15 . 34 k + 14 k - 14$ $= 34 (k^{2} + 1) + 524 k - 48 = 34 . 34 k + 524 k - 48$ $= 1680 k - 48 = 1680 (17 + 12 \sqrt{2}) - 48 = 36 / y^{3}$ $\Leftrightarrow 28512 + 20160 \sqrt{2} = 36 / y^{3}$ $y^{3} = \frac{36}{28512 + 20160 \sqrt{2}} \Rightarrow y =^{3} \sqrt{\frac{1}{792 + 560 \sqrt{2}}}$ $=^{3} \sqrt{\frac{1}{{(6 + 4 \sqrt{2})}^{3}}} = \frac{1}{6 + 4 \sqrt{2}} = \frac{3 - 2 \sqrt{2}}{2}$ $x = (17 + 12 \sqrt{2}) . \frac{3 - 2 \sqrt{2}}{2} = \frac{3 + 2 \sqrt{2}}{2}$ $ii) k = 17 - 12 \sqrt{2} . Similarly, we get$ $y = \frac{3 + 2 \sqrt{2}}{2}, x = \frac{3 - 2 \sqrt{2}}{2}$ $Thus the given system has two solutions$ $(x, y) \in {(\frac{3 - 2 \sqrt{2}}{2}, \frac{3 + 2 \sqrt{2}}{2}), (\frac{3 + 2 \sqrt{2}}{2}, \frac{3 - 2 \sqrt{2}}{2})}$
	Answered by MJS_new last updated on 27/Oct/20
	$in this case it′s easier to let x=p−q∧y=p+q we get { ((4(4p^2 −q^2 )(√(p^2 −q^2 ))=14)),((8p(4p^2 −3q^2 )=36 ⇒ q^2 =((8p^3 −9)/(6p)))) :} insert in first equation (((16p^3 +9)(√(54−12p^3 )))/(9(√p^3 )))=14 squaring and transforming leads to p^9 −((27)/8)p^6 +((27)/(64))p^3 −((729)/(512))=0 (p^3 −((27)/8))(p^6 +((27)/(64)))=0 ⇒ p=(3/2) ⇒ q=±(√2) ⇒ x=(3/2)∓(√2)∧y=(3/2)±(√2)$
	$in this case {it}^{'} s easier to let$ $x = p - q \land y = p + q$ $we get$ ${\begin{cases} 4 (4 p^{2} - q^{2}) \sqrt{p^{2} - q^{2}} = 14 \\ 8 p (4 p^{2} - 3 q^{2}) = 36 \Rightarrow q^{2} = \frac{8 p^{3} - 9}{6 p} \end{cases}$ $insert in first equation$ $\frac{(16 p^{3} + 9) \sqrt{54 - 12 p^{3}}}{9 \sqrt{p^{3}}} = 14$ $squaring and transforming leads to$ $p^{9} - \frac{27}{8} p^{6} + \frac{27}{64} p^{3} - \frac{729}{512} = 0$ $(p^{3} - \frac{27}{8}) (p^{6} + \frac{27}{64}) = 0 \Rightarrow p = \frac{3}{2} \Rightarrow q = \pm \sqrt{2}$ $\Rightarrow x = \frac{3}{2} \mp \sqrt{2} \land y = \frac{3}{2} \pm \sqrt{2}$
	Answered by benjo_mathlover last updated on 27/Oct/20
	$by substituting { ((u=(√x))),((v=(√y))) :} we obtain equivalent form { ((uv(3u^4 +10u^2 v^2 +3v^4 )=14)),((u^6 +15u^4 v^2 +15u^2 v^4 +v^6 =36)) :} Here we should recognize elements of binomial with exponent equal to 6. { ((36+2.14=u^6 +6u^5 v+15u^4 v^2 +20u^3 v^3 +15u^2 v^4 +6uv^5 +v^6 )),((36−2.14=u^6 −6u^5 v+15u^4 v^2 −20u^3 v^3 +15u^2 v^4 −6uv^5 +v^6 )) :} therefore { (((u+v)^6 =64)),(((u−v)^6 =8)) :} which implies { ((u+v=2)),((u−v=(√2))) :} since u,v have to be +ve so { ((u=1+((√2)/2))),((v=1−((√2)/2))) :} ⇔ { (((x,y)=((3/2)+(√2), (3/2)−(√2)))),(((x,y)=((3/2)−(√2), (3/2)+(√2)) )) :}$
	$b y s u b s t i t u t i n g {\begin{cases} u = \sqrt{x} \\ v = \sqrt{y} \end{cases}$ $w e o b t a i n e q u i v a l e n t f o r m$ ${\begin{cases} u v (3 u^{4} + 10 u^{2} v^{2} + 3 v^{4}) = 14 \\ u^{6} + 15 u^{4} v^{2} + 15 u^{2} v^{4} + v^{6} = 36 \end{cases}$ $H e r e w e s h o u l d r e c o g n i z e e l e m e n t s$ $o f b i n o m i a l w i t h e x p o n e n t e q u a l t o 6 .$ ${\begin{cases} 36 + 2.14 = u^{6} + 6 u^{5} v + 15 u^{4} v^{2} + 20 u^{3} v^{3} + 15 u^{2} v^{4} + 6 {u v}^{5} + v^{6} \\ 36 - 2.14 = u^{6} - 6 u^{5} v + 15 u^{4} v^{2} - 20 u^{3} v^{3} + 15 u^{2} v^{4} - 6 {u v}^{5} + v^{6} \end{cases}$ $t h e r e f o r e {\begin{cases} {(u + v)}^{6} = 64 \\ {(u - v)}^{6} = 8 \end{cases}$ $w h i c h i m p l i e s {\begin{cases} u + v = 2 \\ u - v = \sqrt{2} \end{cases} s i n c e u, v h a v e t o b e + v e$ $s o {\begin{cases} u = 1 + \frac{\sqrt{2}}{2} \\ v = 1 - \frac{\sqrt{2}}{2} \end{cases} \Leftrightarrow {\begin{cases} (x, y) = (\frac{3}{2} + \sqrt{2}, \frac{3}{2} - \sqrt{2}) \\ (x, y) = (\frac{3}{2} - \sqrt{2}, \frac{3}{2} + \sqrt{2}) \end{cases}$
	Answered by behi83417@gmail.com last updated on 27/Oct/20
	${ (((3x^2 +3y^2 +10xy)(√(xy))=14)),(((x+y)(x^2 +14xy+y^2 )=36)) :} ⇒_(xy=q^2 ) ^(x+y=p) { (([3(x+y)^2 +4xy](√(xy))=14)),(((x+y)[(x+y)^2 +12xy]=36)) :} ⇒ { ((q.(3p^2 +4q^2 )=14)),((p.(p^2 +12q^2 )=36)) :}⇒(q/p).((3p^2 +4q^2 )/(p^2 +12q^2 ))=(7/(18)) ⇒^((p/q)=t) (1/t).((3t^2 +4)/(t^2 +12))=(7/(18))⇒54t^2 +72=7t^3 +84t ⇒7t^3 −54t^2 +84t−72=0 ⇒(t−6)(7t^2 −12t+12)=0 ⇒ { ((t=(p/q)=6)),((t=((6±(√(36−84)))/7)=((6±4i(√3))/7))) :} (p/q)=6⇒6q^2 (36q^2 +12q^2 )=36⇒q^3 =(1/8) ⇒q=(1/2),p=6q=3⇒ { ((x+y=3)),((xy=q^2 =(1/4))) :} ⇒z^2 −3z+(1/4)=0⇒z=x∨y=((3±(√(9−1)))/2) ⇒x∨y=((3±2(√2))/2)=(3/2)±(√2) .■$
	${\begin{cases} ({3 x}^{2} + {3 y}^{2} + 10 xy) \sqrt{xy} = 14 \\ (x + y) (x^{2} + 14 xy + y^{2}) = 36 \end{cases}$ $\underset{xy = q^{2}}{\overset{x + y = p}{\Rightarrow}} {\begin{cases} [3 {(x + y)}^{2} + 4 xy] \sqrt{xy} = 14 \\ (x + y) [{(x + y)}^{2} + 12 xy] = 36 \end{cases}$ $\Rightarrow {\begin{cases} q . ({3 p}^{2} + {4 q}^{2}) = 14 \\ p . (p^{2} + {12 q}^{2}) = 36 \end{cases} \Rightarrow \frac{q}{p} . \frac{{3 p}^{2} + {4 q}^{2}}{p^{2} + {12 q}^{2}} = \frac{7}{18}$ $\overset{\frac{p}{q} = t}{\Rightarrow} \frac{1}{t} . \frac{{3 t}^{2} + 4}{t^{2} + 12} = \frac{7}{18} \Rightarrow {54 t}^{2} + 72 = {7 t}^{3} + 84 t$ $\Rightarrow {7 t}^{3} - {54 t}^{2} + 84 t - 72 = 0$ $\Rightarrow (t - 6) ({7 t}^{2} - 12 t + 12) = 0$ $\Rightarrow {\begin{cases} t = \frac{p}{q} = 6 \\ t = \frac{6 \pm \sqrt{36 - 84}}{7} = \frac{6 \pm 4 i \sqrt{3}}{7} \end{cases}$ $\frac{p}{q} = 6 \Rightarrow {6 q}^{2} ({36 q}^{2} + {12 q}^{2}) = 36 \Rightarrow q^{3} = \frac{1}{8}$ $\Rightarrow q = \frac{1}{2}, p = 6 q = 3 \Rightarrow {\begin{cases} x + y = 3 \\ xy = q^{2} = \frac{1}{4} \end{cases}$ $\Rightarrow z^{2} - 3 z + \frac{1}{4} = 0 \Rightarrow z = x \lor y = \frac{3 \pm \sqrt{9 - 1}}{2}$ $\Rightarrow x \lor y = \frac{3 \pm 2 \sqrt{2}}{2} = \frac{3}{2} \pm \sqrt{2} . ◼$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum