
Question and Answers Forum
Question Number 125202 by bemath last updated on 09/Dec/20
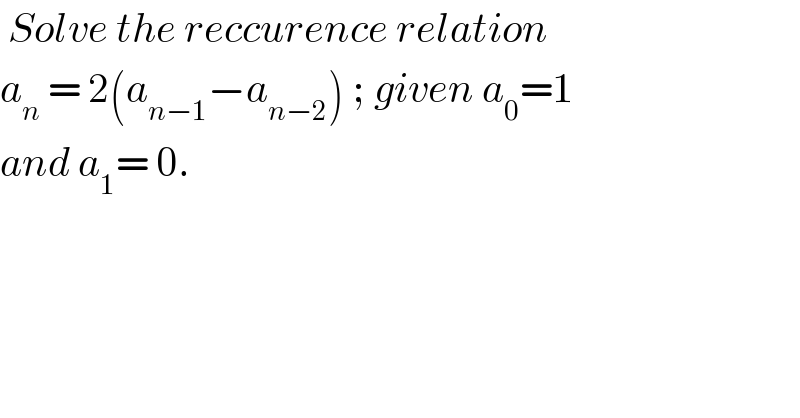
Answered by liberty last updated on 09/Dec/20
![The characteristic equation :≡ x^2 −2x+2=0 and have the roots are { ((α=1+i)),((α^− = 1−i)) :} Expressing α and α^− in trigonometric form we have { ((α=(√2) (cos (π/4)+ i sin (π/4)))),((α^− = (√2) (cos (π/4)−i sin (π/4)))) :} The general solution is a_n = P (α)^n +Q(α^− )^n by the Moivre′s Theorem give a_n = ((√2))^n [ P(cos ((nπ)/4)+i sin ((nπ)/4))+Q(cos ((nπ)/4)−i sin ((nπ)/4)) ] a_n = ((√2))^n [ (P+Q)cos ((nπ)/4)+(P−Q)i sin ((nπ)/4) ] The initial condition imply that { ((P+Q=1)),(((√2) (((√2)/2) (P+Q)+((√2)/2) (P−Q)i)=0)) :} we get (P−Q)i = −1 thus the required solution given by a_n = ((√2))^n (cos ((nπ)/4)−sin ((nπ)/4)); for n ≥ 0](Q125203.png)
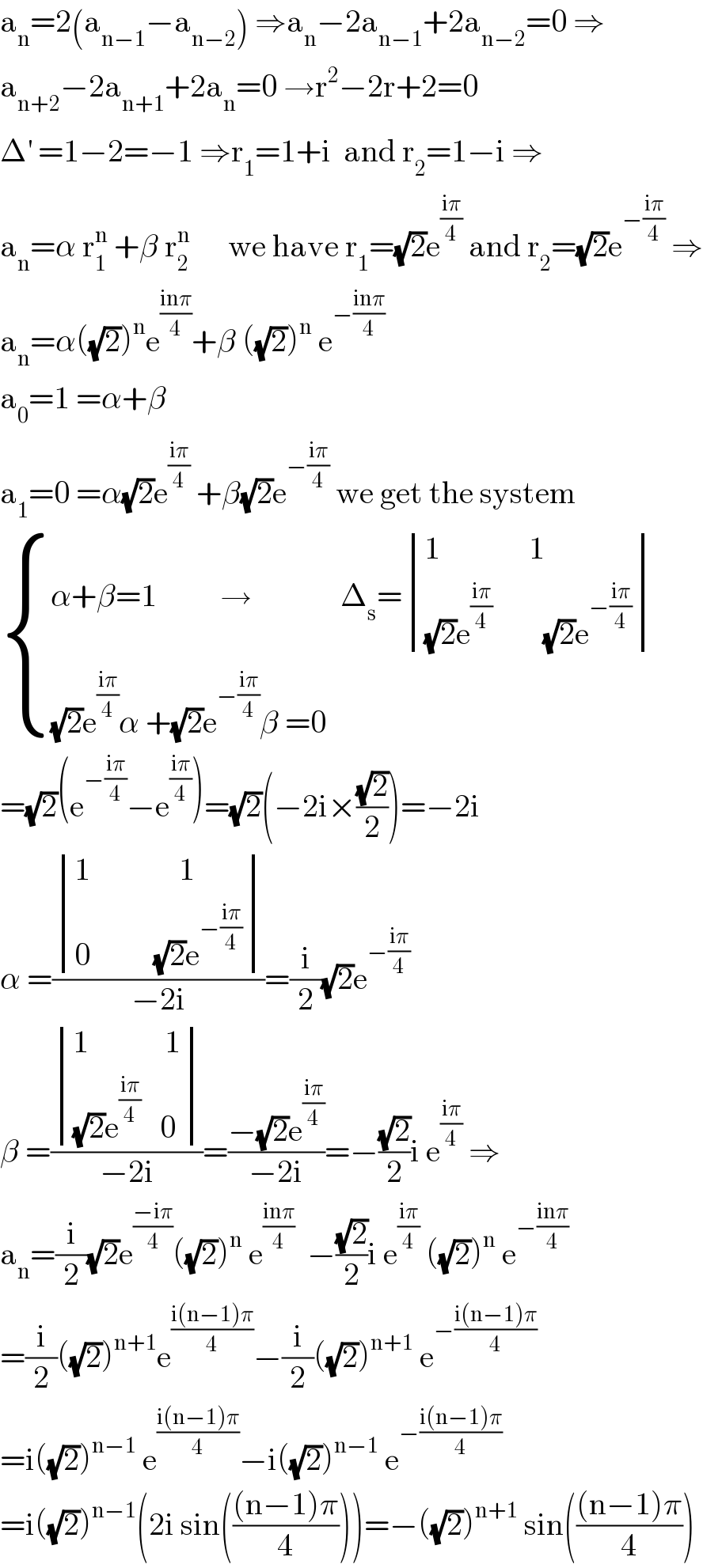
Answered by mathmax by abdo last updated on 09/Dec/20
| ||
Question and Answers Forum | ||
Question Number 125202 by bemath last updated on 09/Dec/20 | ||
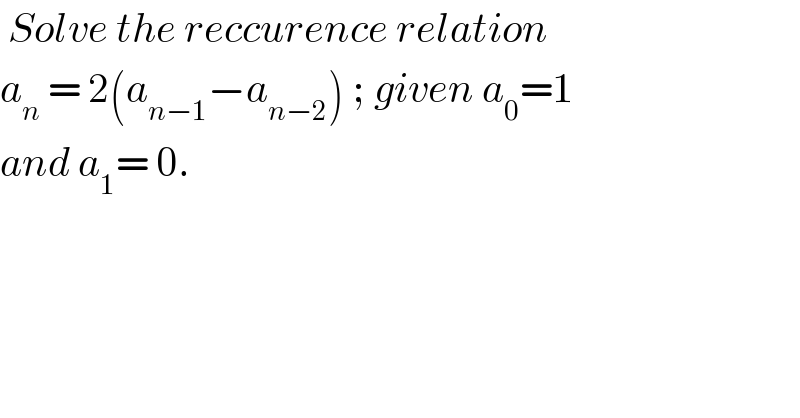 | ||
Answered by liberty last updated on 09/Dec/20 | ||
![The characteristic equation :≡ x^2 −2x+2=0 and have the roots are { ((α=1+i)),((α^− = 1−i)) :} Expressing α and α^− in trigonometric form we have { ((α=(√2) (cos (π/4)+ i sin (π/4)))),((α^− = (√2) (cos (π/4)−i sin (π/4)))) :} The general solution is a_n = P (α)^n +Q(α^− )^n by the Moivre′s Theorem give a_n = ((√2))^n [ P(cos ((nπ)/4)+i sin ((nπ)/4))+Q(cos ((nπ)/4)−i sin ((nπ)/4)) ] a_n = ((√2))^n [ (P+Q)cos ((nπ)/4)+(P−Q)i sin ((nπ)/4) ] The initial condition imply that { ((P+Q=1)),(((√2) (((√2)/2) (P+Q)+((√2)/2) (P−Q)i)=0)) :} we get (P−Q)i = −1 thus the required solution given by a_n = ((√2))^n (cos ((nπ)/4)−sin ((nπ)/4)); for n ≥ 0](Q125203.png) | ||
| ||
Answered by mathmax by abdo last updated on 09/Dec/20 | ||
 | ||
| ||