The roots of the equation 2x^2 − x + 3 = 0 are α and β if the roots of 3x^2 + px + q=0 are α + (1/α) and β + (1/(β )) find the value of p and q.


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 38012 by Rio Mike last updated on 20/Jun/18

$T h e r o o t s o f t h e e q u a t i o n$ $2 x^{2} - x + 3 = 0 a r e α a n d β$ $i f t h e r o o t s o f 3 x^{2} + p x + q = 0$ $a r e α + \frac{1}{α} a n d β + \frac{1}{β} f i n d t h e v a l u e$ $o f p a n d q .$
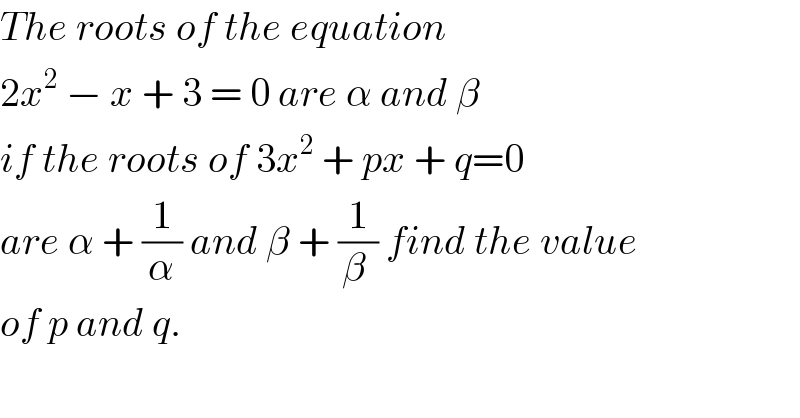
Commented by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18

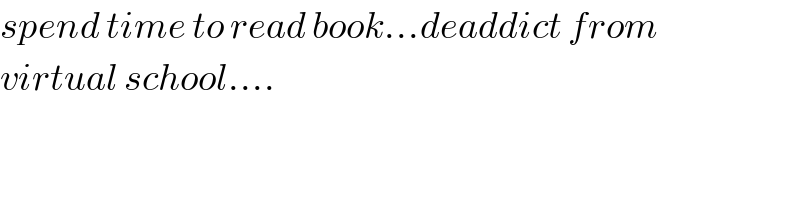
$s p e n d t i m e t o r e a d b o o k . . . d e a d d i c t f r o m$ $v i r t u a l s c h o o l . . . .$
	Answered by MJS last updated on 20/Jun/18

	$2 x^{2} - x + 3 = 0$ $x = \frac{1}{4} \pm \sqrt{\frac{1}{16} - \frac{3}{2}} = \frac{1}{4} \pm \frac{\sqrt{23}}{4} i$ $α = \frac{1}{4} - \frac{\sqrt{23}}{4} i \Rightarrow \frac{1}{α} = \frac{1}{6} + \frac{\sqrt{23}}{6} i \Rightarrow α + \frac{1}{α} = \frac{5}{12} - \frac{\sqrt{23}}{12} i$ $β = \frac{1}{4} + \frac{\sqrt{23}}{4} i \Rightarrow \frac{1}{β} = \frac{1}{6} - \frac{\sqrt{23}}{6} i \Rightarrow β + \frac{1}{β} = \frac{5}{12} + \frac{\sqrt{23}}{12} i$ $3 (x - \frac{5}{12} + \frac{\sqrt{23}}{12} i) (x - \frac{5}{12} - \frac{\sqrt{23}}{12} i) =$ $= 3 x^{2} - \frac{5}{2} x + 1$ $p = - \frac{5}{2}$ $q = 1$
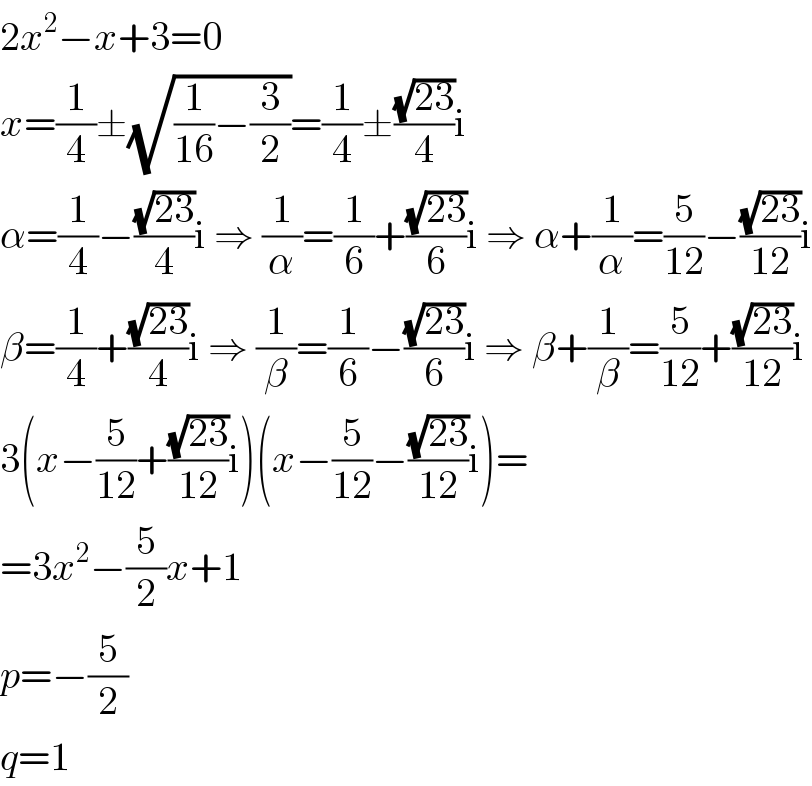
	Answered by ajfour last updated on 20/Jun/18

	$α β = \frac{3}{2}, α + β = \frac{1}{2}$ $(α + \frac{1}{α}) (β + \frac{1}{β}) = \frac{q}{3}$ $α + β + \frac{1}{α} + \frac{1}{β} = - \frac{p}{3}$ $. . . . . . . . .$ $\Rightarrow α β + \frac{α}{β} + \frac{β}{α} + \frac{1}{α β} = \frac{q}{3}$ $(α + β) + \frac{α + β}{α β} = - \frac{p}{3}$ $\frac{3}{2} + \frac{{(\frac{1}{2})}^{2} - 2 (\frac{3}{2})}{\frac{3}{2}} + \frac{2}{3} = \frac{q}{3}$ $a n d \frac{1}{2} + \frac{(\frac{1}{2})}{(\frac{3}{2})} = - \frac{p}{3}$ $q = 3 [\frac{3}{2} - \frac{11}{6} + \frac{2}{3}] = 1$ $p = - 3 [\frac{1}{2} + \frac{1}{3}] = - \frac{5}{2} .$
	Answered by tanmay.chaudhury50@gmail.com last updated on 20/Jun/18

	$α + β = \frac{1}{2} α β = \frac{3}{2}$ $α + \frac{1}{α} + β + \frac{1}{β} = \frac{- p}{3}$ $α + β + \frac{α + β}{α β} = \frac{- p}{3}$ $\frac{1}{2} + \frac{1}{2} \times \frac{2}{3} = - \frac{p}{3}$ $\frac{5}{6} = - \frac{p}{3}$ $p = - \frac{5}{2}$ $(α + \frac{1}{α}) \times (β + \frac{1}{β}) = \frac{q}{3}$ $α β + \frac{α}{β} + \frac{β}{α} + \frac{1}{α β} = \frac{q}{3}$ $α β + \frac{1}{α β} + \frac{α^{2} + β^{2}}{α β} = \frac{q}{3}$ $\frac{3}{2} + \frac{2}{3} + \frac{{(α + β)}^{2} - 2 α β}{α β} = \frac{q}{3}$ $\frac{13}{6} + \frac{\frac{1}{4} - 2 \times \frac{3}{2}}{\frac{3}{2}} = \frac{q}{3}$ $\frac{13}{6} + \frac{\frac{1 - 12}{4}}{\frac{3}{2}} = \frac{q}{3}$ $\frac{13}{6} - \frac{11 \times 2}{12} = \frac{q}{3}$ $\frac{13 - 11}{6} = \frac{q}{3}$ $q = 1$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum