Question and Answers Forum
Question Number 88372 by mr W last updated on 10/Apr/20

Commented by mr W last updated on 10/Apr/20

Commented by mr W last updated on 10/Apr/20

Commented by jagoll last updated on 10/Apr/20
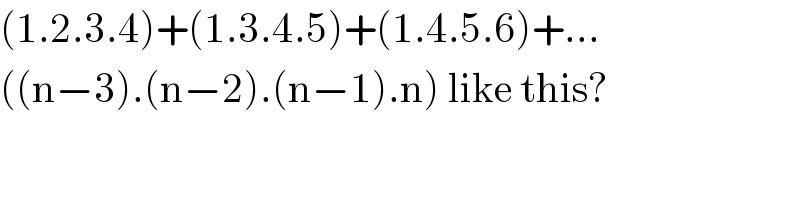
Commented by mr W last updated on 10/Apr/20

Commented by jagoll last updated on 10/Apr/20
Commented by Tony Lin last updated on 10/Apr/20
![first consider Σ_(a≠b) ab Σ_(a≠b) ab =1×2+1×3+∙∙∙+1×n +2×1+2×3+∙∙∙+2×n ∙∙∙ +n×1+n×2+∙∙∙+n(n−1)r =1[((n(n+1))/2)]−1^2 +2[((n(n+1))/2)]−2^2 +∙∙∙ +n[((n(n+1))/2)]−n^2 =[((n(n+1))/2)]^2 −((n(n+1)(2n+1))/6) =((n(n−1)(n+1)(3n+2))/(12)) Σ_(a≠b≠c) abc =1×2×3+1×2×4+∙∙∙+1×2×n +1×3×2+1×3×4+∙∙∙+1×n(n−1) ∙∙∙ +1×n×2+1×n×3+∙∙∙+1×n(n−1) ∙∙∙and Σ2×∙∙∙ Σ3×∙∙∙ to Σn×∙∙∙ =((n(n−1)(n+1)(3n+2))/(12))−2[((n(n+1))/2)−1^2 ] +((n(n−1)(n+1)(3n+2))/(12))−2[((2n(n+1))/2)−2^2 ] ∙∙∙ +((n(n−1)(n+1)(3n+2))/(12))−2[((n^2 (n+1))/2)−n^2 ] =((n^2 (n−1)(n+1)(3n+2))/(12))−((2n(n−1)(n+1)(3n+2))/(12)) =((n(n−1)(n−2)(n+1)(3n+2))/(12)) Σ_(a≠b≠c≠d) abcd =1×2×3×4+1×2×3×5+∙∙∙+1×2×3×n +1×2×4×3+1×2×4×5+∙∙∙+1×2×4×n ∙∙∙ +1×2×n×3+1×2×n×4+∙∙∙+1×2×n(n−1) ∙∙∙and Σ1×3×∙∙∙to Σ1×n×∙∙∙ and Σ2×∙∙∙ to Σn×∙∙∙ =((n(n−1)(n−2)(n+1)(3n+2))/(12)) −3{((n(n−1)(n+1)(3n+2))/(12))−2[((n(n+1))/2)−1^2 ]} +((n(n−1)(n−2)(n+1)(3n+2))/(12)) −3{((n(n−1)(n+1)(3n+2))/(12))−2[((2n(n+1))/2)−2^2 ] +∙∙∙ =((n^2 (n−1)(n−2)(n+1)(3n+2))/(12)) −3[((n^2 (n−1)(n+1)(3n+2))/(12))−((2n(n−1)(n+1)(3n+2))/(12))] =((n^2 (n−1)(n−2)(n+1)(3n+2))/(12)) − ((3n(n−1)(n−2)(n+1)(3n+2))/(12)) =((n(n−1)(n−2)(n−3)(n+1)(3n+2))/(12)) from the rule Σ_(a_1 ≠a_2 ≠a_3 ∙∙∙≠a_k ) Π_(j=1) ^k a_j ,1<k<n =((P_k ^n (n+1)(3n+2))/(12)) , P_k ^n =C_k ^n ×k!](Q88387.png)
Commented by Tony Lin last updated on 10/Apr/20
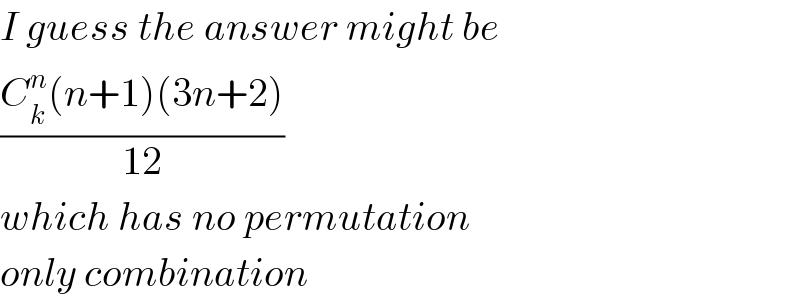
Commented by mr W last updated on 10/Apr/20
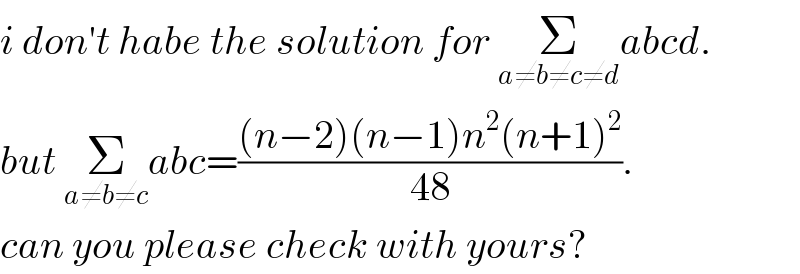
Commented by Tony Lin last updated on 10/Apr/20
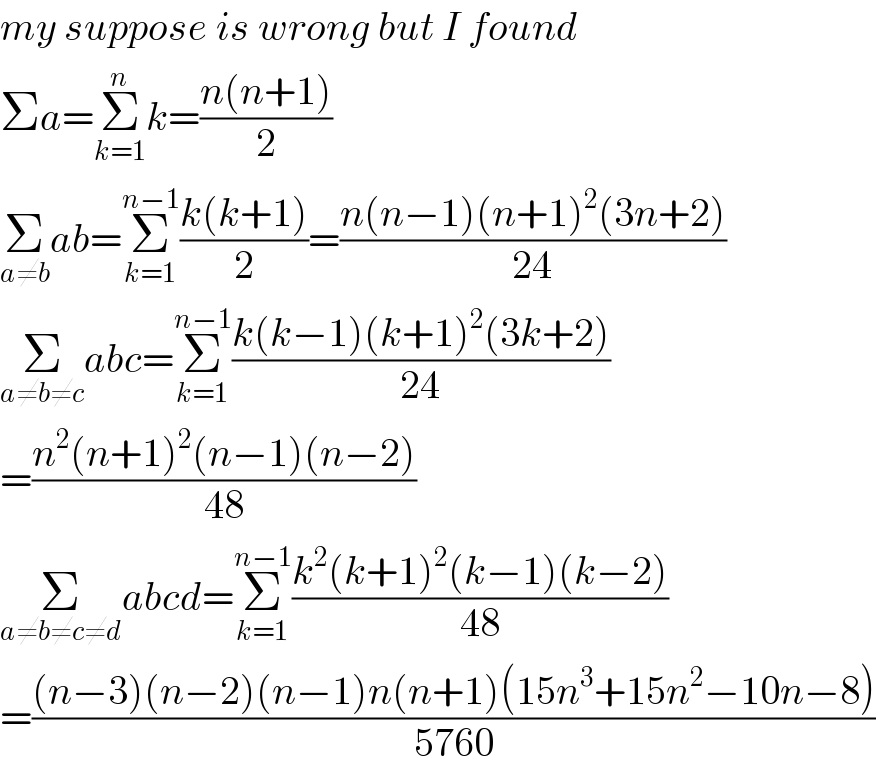
Commented by mr W last updated on 10/Apr/20