
Question and Answers Forum
Question Number 123866 by benjo_mathlover last updated on 28/Nov/20

Answered by liberty last updated on 28/Nov/20
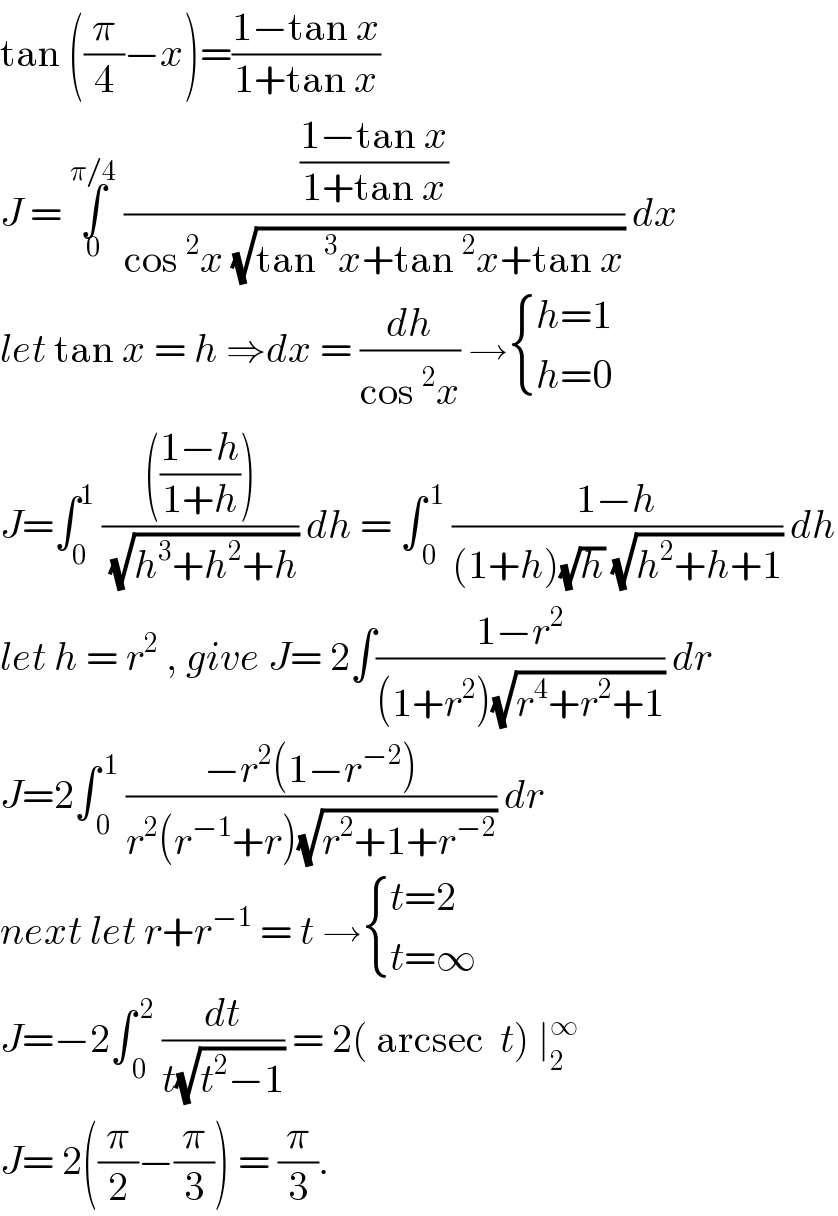
Answered by MJS_new last updated on 29/Nov/20
![tan ((π/4)−x) =((1−tan x)/(1+tan x)) cos^2 x =(1/(1+tan^2 x)) let me write τ for tan x now we have −∫_0 ^(π/4) (((τ−1)(τ^2 +1))/((τ+1)(√(τ(τ^2 +τ+1)))))dx= =[t=((√τ)/( (√(τ^2 +τ+1)))) → dx=−((2(τ^2 +τ+1)^(3/2) (√τ))/((τ^2 −1)(τ^2 +1)))dt] =2∫_0 ^((√3)/3) ((τ^2 +τ+1)/((τ^2 +1)^2 ))dt= [τ=tan x =−((t^2 −1−(√(−3t^4 −2t^2 +1)))/(2t^2 ))] =2∫_0 ^((√3)/3) (dt/(t^2 +1))=2arctan t =(π/3) [2arctan t =arccos ((1−t^2 )/(1+t^2 )) =arccos (1/(1+sin 2x))]](Q123941.png)
| ||
Question and Answers Forum | ||
Question Number 123866 by benjo_mathlover last updated on 28/Nov/20 | ||
 | ||
Answered by liberty last updated on 28/Nov/20 | ||
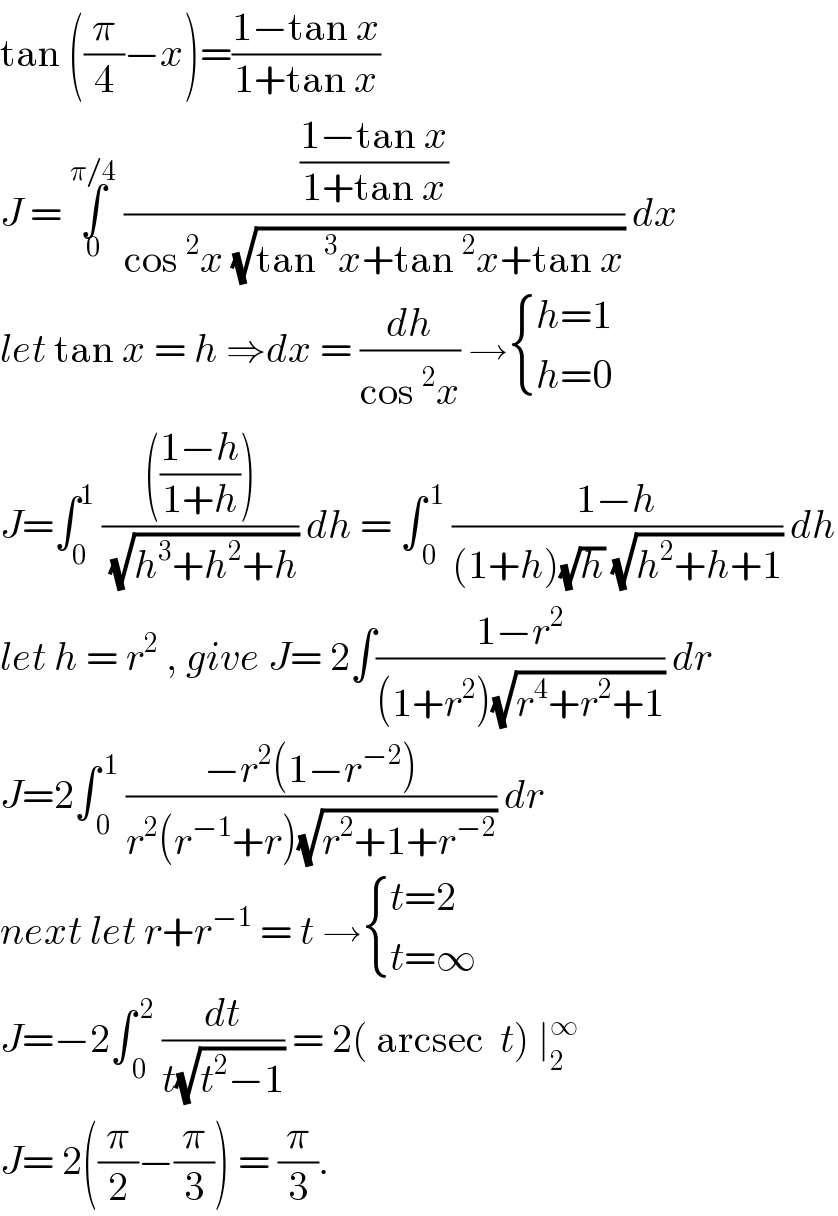 | ||
| ||
Answered by MJS_new last updated on 29/Nov/20 | ||
![tan ((π/4)−x) =((1−tan x)/(1+tan x)) cos^2 x =(1/(1+tan^2 x)) let me write τ for tan x now we have −∫_0 ^(π/4) (((τ−1)(τ^2 +1))/((τ+1)(√(τ(τ^2 +τ+1)))))dx= =[t=((√τ)/( (√(τ^2 +τ+1)))) → dx=−((2(τ^2 +τ+1)^(3/2) (√τ))/((τ^2 −1)(τ^2 +1)))dt] =2∫_0 ^((√3)/3) ((τ^2 +τ+1)/((τ^2 +1)^2 ))dt= [τ=tan x =−((t^2 −1−(√(−3t^4 −2t^2 +1)))/(2t^2 ))] =2∫_0 ^((√3)/3) (dt/(t^2 +1))=2arctan t =(π/3) [2arctan t =arccos ((1−t^2 )/(1+t^2 )) =arccos (1/(1+sin 2x))]](Q123941.png) | ||
| ||