
Question and Answers Forum
Question Number 66279 by gunawan last updated on 12/Aug/19
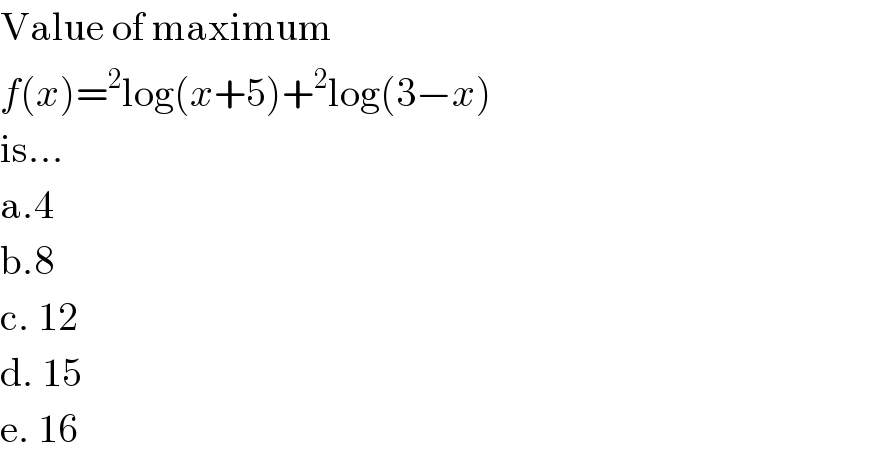
Commented by mathmax by abdo last updated on 12/Aug/19
![f(x)=log_2 (x+5)+log_2 (3−x) x∈D_f ⇔x+5>0 and 3−x>0 ⇔−5<x<3 ⇒D_f =]−5,3[ f(x) =(1/(ln(2))){ln(x+5)+ln(3−x)} ⇒f^′ (x)=(1/(ln2)){(1/(x+5))−(1/(3−x))} =(1/(ln2)){((3−x−x−5)/((x+5)(3−x)))} =(1/(ln(2))){((−2−2x)/((x+5)(3−x)))} =((−2)/(ln2)){((x+1)/((x+5)(3−x)))} so f^′ (x)=0 ⇔x=−1 variation of f(x) x −5 −1 3 f^′ (x) + 0 − f(x) −∞ inc f(−1)decr −∞ max f(x)= f(−1)=(1/(ln(2))){2ln(2)+2ln(2)} =4 x∈D_f the correct answer is a)](Q66284.png)
Answered by Kunal12588 last updated on 12/Aug/19
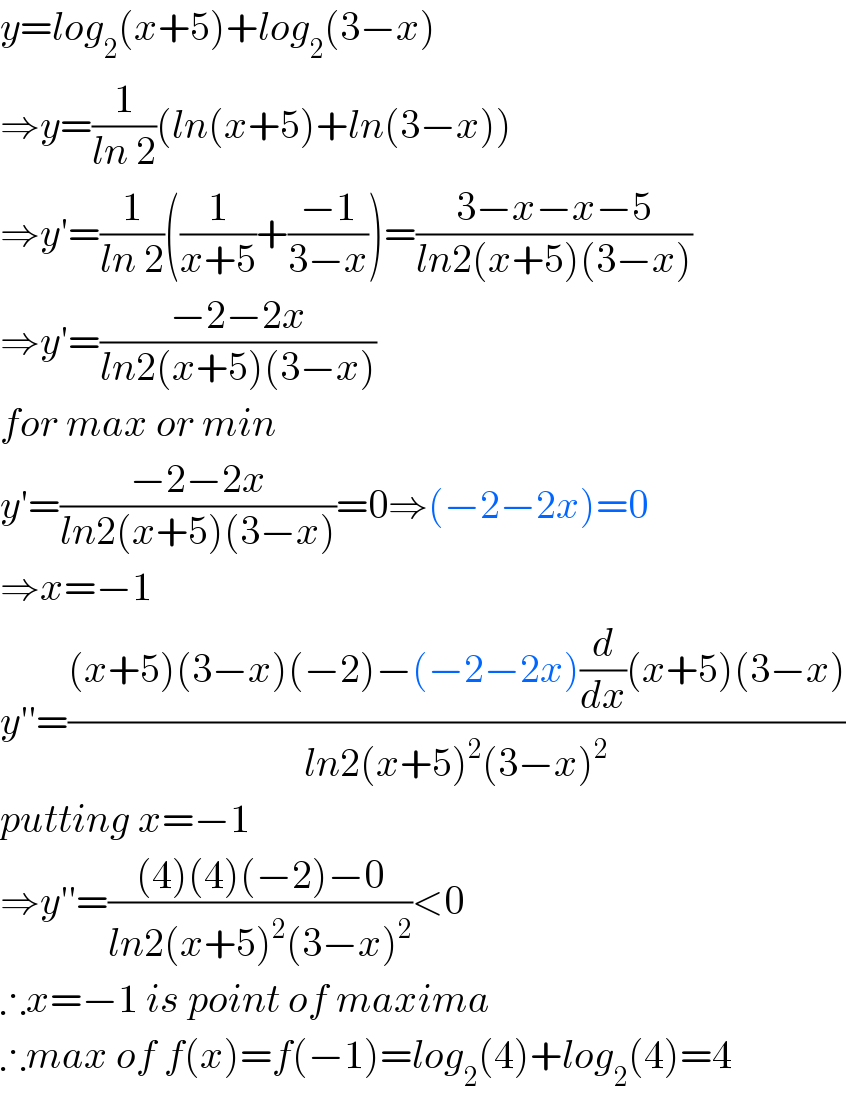
| ||
Question and Answers Forum | ||
Question Number 66279 by gunawan last updated on 12/Aug/19 | ||
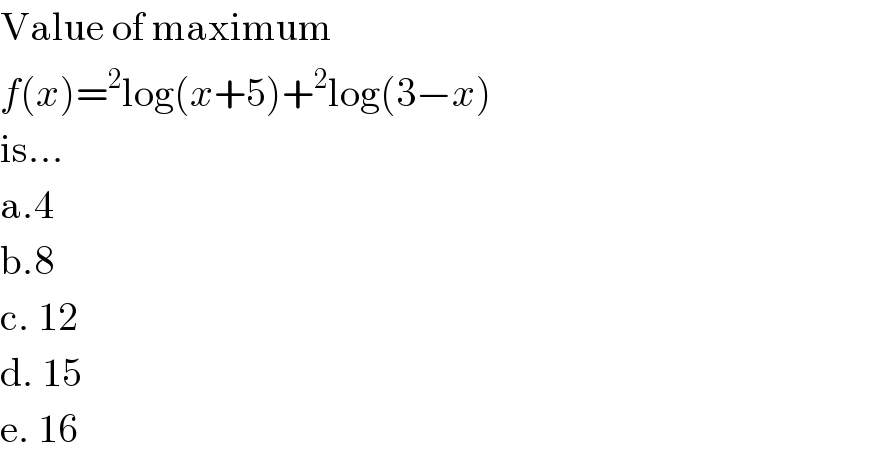 | ||
Commented by mathmax by abdo last updated on 12/Aug/19 | ||
![f(x)=log_2 (x+5)+log_2 (3−x) x∈D_f ⇔x+5>0 and 3−x>0 ⇔−5<x<3 ⇒D_f =]−5,3[ f(x) =(1/(ln(2))){ln(x+5)+ln(3−x)} ⇒f^′ (x)=(1/(ln2)){(1/(x+5))−(1/(3−x))} =(1/(ln2)){((3−x−x−5)/((x+5)(3−x)))} =(1/(ln(2))){((−2−2x)/((x+5)(3−x)))} =((−2)/(ln2)){((x+1)/((x+5)(3−x)))} so f^′ (x)=0 ⇔x=−1 variation of f(x) x −5 −1 3 f^′ (x) + 0 − f(x) −∞ inc f(−1)decr −∞ max f(x)= f(−1)=(1/(ln(2))){2ln(2)+2ln(2)} =4 x∈D_f the correct answer is a)](Q66284.png) | ||
Answered by Kunal12588 last updated on 12/Aug/19 | ||
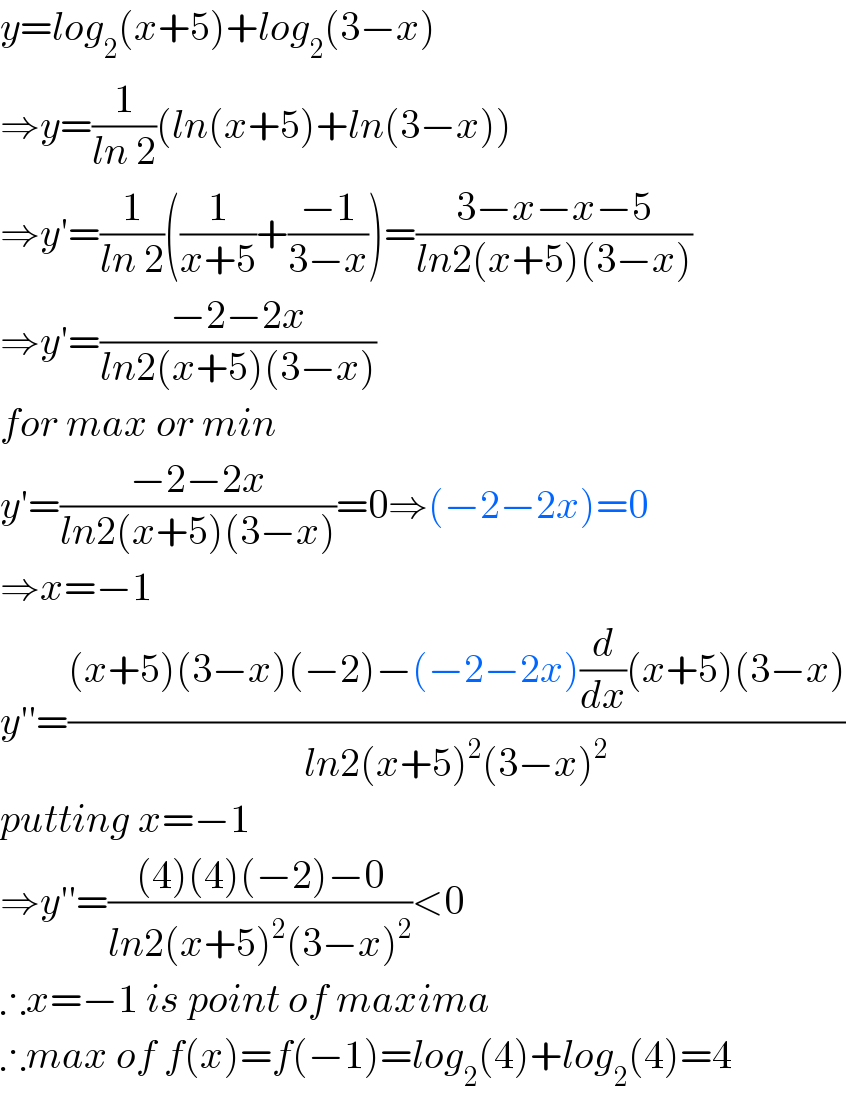 | ||
| ||