
Question and Answers Forum
VectorQuestion and Answers: Page 3



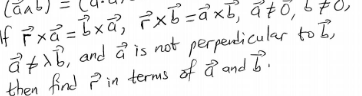



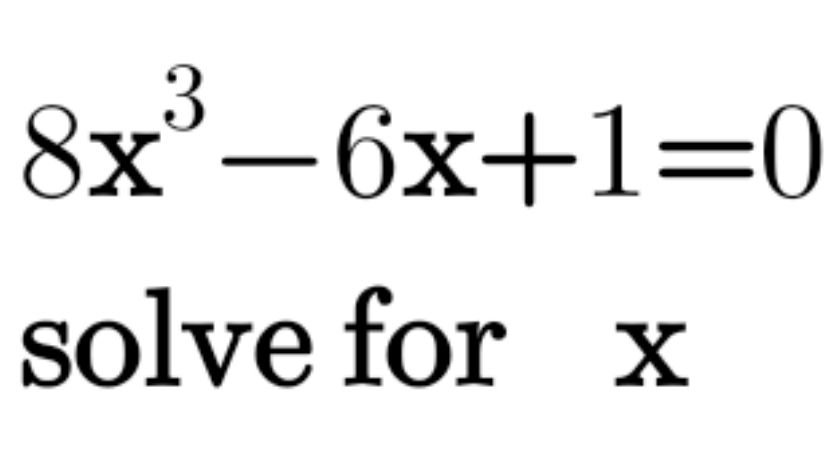


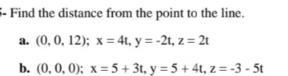

|
Question and Answers Forum |
VectorQuestion and Answers: Page 3 |
| ∫_0 ^2 ∫_0 ^3 ∫_0 ^4 e^(x+y+z) dx dy dz=? |

|
| if 2x+(1/( (√x)))=(1/2) find the value 8x+(1/( (√x)))=? |
| Send you solutions to kinmatics@gmail.com |

|

|
| The points A, B and C have position vectors a, b and c respectively reffrred to an origin O. i. Given that the point X lie on AB produced so that AB : BX=2:1, find x, the position vector of X in terms of b and c. ii. if Y lies on BC, between B and C so that BY : YC = 1:3, find y, the position vector of Y in terms of b and c. iii. Given that Z is the mid point of AC, show that X, Y and Z are collinear. |
| Θ =∫_0 ^( ∞) ∫_0 ^( ∞) xy e^( −(x+y)) cos(x+y )dxdy=(1/σ) find the value of ” σ ”. |
| lim_(x→0) (1/x) [ ((((1−(√(1−x)))/( (√(1+x))−1)) ))^(1/3) −1 ]=? |
| ∣a^→ ∣=1 ∣b^→ ∣=2 ∢(a^→ , b^→ )=(π/3) ∣a^→ +b^→ ∣=? |
| ∣a^→ ∣=13 ∣b^→ ∣=19 ∣a^→ +b^→ ∣=24 ∣a^→ −b^→ ∣=? |
| ∫cos(x^7 )dx = |
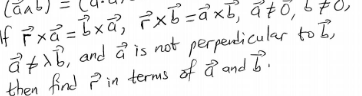
|
| check that the function u(x,t) = exp{−((n^2 α^2 π^2 )/L^2 )t} sin((nπx)/L) n = 1,2,... satisfy the heat equation heat equation α^2 (∂^2 u/∂x^2 ) = (∂u/∂t), 0 < x < L |

|

|

|
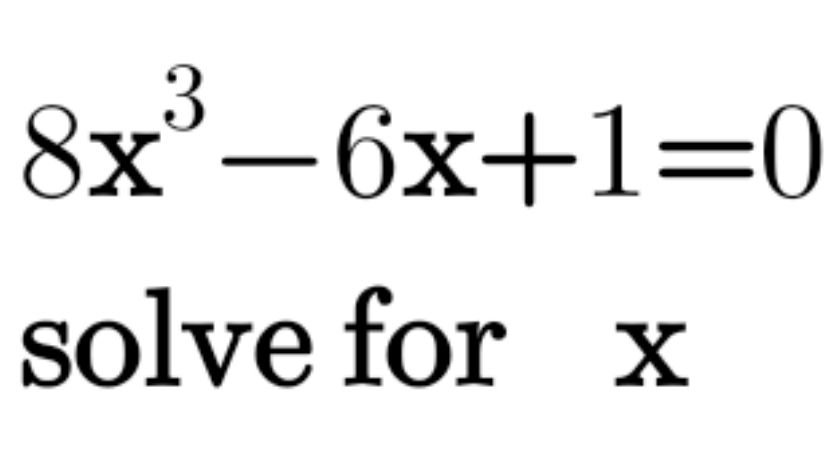
|

|

|
| ∫ e^(tan(x)) dx {Z.A} |
| A ector field is given by v= (x^2 −y^2 +x)i−(2xy+y)j. Show that vector v is irrotational hence find the scalar potential |
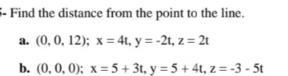
|
| lim_(x→∞) ((1/(x^2 +1))+(1/(x^2 +4))+(1/(x^2 +9))+…)=? |
| determine the angle between two vectors A=4ax+ay−3az and B=2ax+4ay−3az |

|