
Question and Answers Forum
VectorQuestion and Answers: Page 4


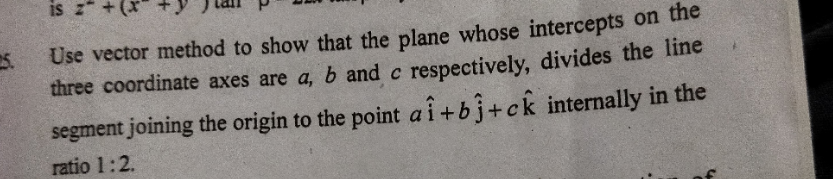








|
Question and Answers Forum |
VectorQuestion and Answers: Page 4 |

|
| 0< α <(π/2) (( sin(α)))^(1/( 3)) + ((cos(α))^(1/3) )= (( tan(α)))^(1/3) (( tan (α ) + cot (α ))/2) =? |
| ∫_(−1 ) ^1 ((3x+4)/(3+4x+3x^2 ))dt please,help me |

|
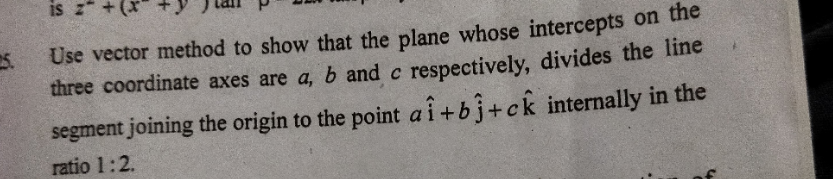
|
| Ω := ∫_0 ^( 1) Li_( 2) ( (√x) )dx = ? |

|

|

|

|
| let f(x,y)=((x^5 y^2 )/(10)) then find D_u f(−5,−3) in the direction of the vector <0,−2>? |
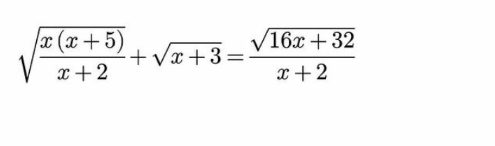
|
| Given p^→ =(√2) i^ +2(√3) j^ + (√3) k^ & q^→ =a i^ +j^ +2k^ . If proj_q^→ p^→ = ((2(√2))/9) q^→ then ∣q^→ ∣ =? |

|

|
| ..........CALCULUS........... prove that:: 𝛗:=Σ_(n=1) ^∞ (((−1)^(n−1) ((n−1)!)^2 )/((2n)!))=2log^2 (ϕ) ϕ=golden ratio.... ............. |

|
| Let f(x)=((sin(x))/x) , prove that : Σ_(n=0) ^∞ [ f(nπ+α)+f(nπ−α) ]= 1+f(α) |

|

|
| For what values of λ are the vectors λi^ + 2j^ + k^ , 3i^ +4j^ +λk^ , j^ + k^ coplanar |
| Vector let L_1 = AC where A=(2,−1,3) and C=(1,0,−5)and let L_2 = BD where B=(1,3,0) and D=(3,−4,1). Determine the distance between L_1 and L_2 . |
| Find the coordinates of (−2,0) when the axes are rotated counterclockwise through the angle arcsin (4/5). |
| If three vector a^→ , b^→ and c^→ are such that a^→ ≠ 0 and a^→ ×b^→ = 2(a^→ ×c^→ ) ,∣a^→ ∣ = ∣c^→ ∣ = 1 , ∣b^→ ∣ = 4 and the angle between b^→ and c^→ is cos^(−1) ((1/4)), then b^→ −2c^→ = λ a^→ , where λ =? |
| Let V be a vector space of polynomials p(x)= a+bx+cx^2 with real coefficients a,b and c. Define an inner product on V by (p,q)=(1/2)∫_(−1) ^1 p(x)q(x) dx . (a) Find a orthonormal basis for V consisting of polynomials φ_o (x) , φ_1 (x) and φ_2 (x) having degree 0,1 and 2 respectively. |

|