
Question and Answers Forum
VectorQuestion and Answers: Page 5










|
Question and Answers Forum |
VectorQuestion and Answers: Page 5 |

|
| # calculus# evaluate: 𝛗:=Σ_(k=1) ^∞ (((−1)^(k−1) Γ ((k/2)))/(k Γ(((k+1)/2)))) =? |

|
| If x^2 +x^(−2) =(√(2+(√(2+(√2))))) x^(16) +x^(−16) =? Any help |
| Prove that ▽^2 𝛗=−4𝛑Gρ φ=Potential of Gravitational field ρ=Density G=Universal Gravitational Constant |
| Let vector a^→ , b^→ and c^→ such that ∣a^→ ∣=∣b^→ ∣=((∣c^→ ∣)/2) and a^→ ×(a^→ ×c^→ )+b^→ =0 find the acute angle between a^→ and c^→ . |
| Vector Three vectors satisfy a.b = b.c = c.a = -1 and a + b + c = 0. What is the magnitude of vector a, b , and c? |
| ....nice ..... calculus.... prove that :: 𝛗=∫_0 ^( 1) (((ln(1−x))/(1−(√(1−x)))))dx=4(1−ζ(2)) |
| Find the component form of the vector that reprecents the velocity of an airplane descending at speed of 150 miles per hour at angle 20° below the horizontal |
| If a^→ =(4,2,−1), b^→ =(m,1,1) c^→ =(3^ −1,0) are three vectors then find the value of m such that a^→ ,b^→ and c^→ are coplanar and find a^→ ×(b^→ ×c^→ ). |
| Given vector a^→ = i^ −2j^ +k^ , b^→ = 2i^ +j^ −2k^ , c^→ =−i^ +3j^ −k^ and d^→ = 2j^ −2k^ . Find the value of (a^→ ×b^→ )×(c^→ ×d^→ ). |
| .....#advanced ............... calculus#..... prove that ::: 𝛗=∫_0 ^( 1) ((ln^2 (1−x))/x)dx=^? 2ζ(3) =^(1−x=t) ∫_0 ^( 1) ((ln^2 (t))/(1−t))dt=∫_0 ^( 1) Σ_(n=0) ^∞ ln^2 (t).t^n dt =Σ_(n=0) ^∞ {[(t^(n+1) /(n+1))ln^2 (t)]_0 ^1 −(2/(n+1))∫_0 ^( 1) t^n ln(t) =−2Σ_(n=0) ^∞ (1/(n+1)){[(t^(n+1) /(n+1))ln(t)]_0 ^1 −(1/(n+1))∫_0 ^( 1) t^n dt} =2Σ_(n=0) ^∞ (1/((n+1)^3 ))=2Σ_(n=1) ^∞ (1/n^3 )=2ζ(3) .................... 𝛗=2ζ(3) .................... ..........m.n.july.1970......... |
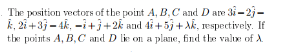
|

|
| lim_(x→0) ((2sin x−sin 2x)/(x−sin x)) |
| Given vector a^→ = i^ +j^ +k^ , c^→ =j^ −k^ ; a^→ × b^→ = c^→ and a^→ .b^→ = 3 then ∣b^→ ∣ = ? |
| Find the point on the paraboloid z = x^2 +y^2 which is closest to the point (3,−6,4 ) |

|

|

|

|
| ... advanced mathematcs ... prove that:: Σ_(n=1) ^∞ (((−1)^n )/(1+n^2 )) =((csch(π)−1)/2) |

|

|

|
| If p^→ =2i^ +5j^ +6k^ q^→ =3i^ +6j^ +8k^ r^→ =2i^ +6j^ +10k^ find p^→ ×q^→ ×r^→ ? |