
Question and Answers Forum
Vector CalculusQuestion and Answers: Page 2











|
Question and Answers Forum |
Vector CalculusQuestion and Answers: Page 2 |
| We know that vertex form of parabola is given as y = a(x−h)^2 +k From the given diagram of bridge that resembles a parabola, we have a vertex points of (0, 30) and other points due to towers that supports the parabolic−shape cable, which is (200, 150). ∴ y = a(x−0)^2 +30 = ax^2 +30 To find the value of ′a′, let′s use the given points other than vertex 150 = a(200)^2 + 30 150−30 = 40000a a = ((120)/(40,000)) = (3/(1000)) ∴ y = ((3x^2 )/(1000)) +30 Also, since we′re asked to find a function that gives a length of metal rod needed relative to its distance from the midpoint of the bridge, with each rods have an equal distance to each other, then we must consider another variable ′d′ that represents the equal distance of metal rods relative to its decided quantity and variable ′n′ given as positive integer that divides the distance of midpoint to tower. d = ((200)/n) ⇒ nd = 200 Example: Engineers decided to use 8 metal rodus, then we have d = ((200)/8) = 25 To calculate the length of each rods, let′s use the formula above First rod: y = ((3(0∙25)^2 )/(1000)) +30 = 30 ft. Second rod: y = ((3(1∙25)^2 )/(1000)) +30 = 31.875 ft. Third rod: y = ((3(2∙25)^2 )/(1000)) +30 = 37.5 ft. Fourth rod: y = ((3(3∙25)^2 )/(1000)) +30 = 46.875 ft. |
| The plane y=1 slices the surface z=arctan(((x+y)/(1−xy))) in a curve C. Find the slope of the tangent line to C at x=2 |

|

|
| If f(z) = z sin(z) + ∣z∣^2 , verify if f(z) satisfy cauchy rieman condition |

|
| sin(x)=a, a∈ |
| (Level - 2) 10th maths assignment of polynomials by PP sir Defind upwards and downwards parabolas. |
| State the asymptotes of the curve y^2 = ((3x^2 )/(x−4)) |

|

|
| What is the volume of tetrahedron ABCD, whose vertices have the coordinates A (2, 3, 6), B (3, 2, 2), C (3, 4, 7) and D (5, 1, 8). Find the lateral surface area of the tetrahedron and find the volume of the tetrahedron? |
| Locate the critical points of the following functions and state the nature of each. (1) f(x,y)=3x^4 −2x^2 +2xy−x+3y^2 −6y+15 (2) f(x,y)=x^2 −4xy+y^2 |

|

|

|

|
| Show that the plane 2x−2y+z+12=0 touches the sphere x^2 +y^2 +z^2 −2x−4y+2z−3=0 Find the point of contact . |
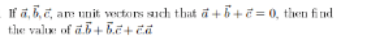
|

|
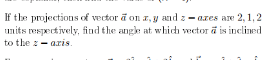
|
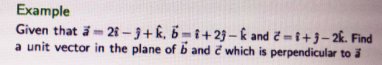
|
| Find the angle between the line ((x−2)/3)= ((y+1)/(−1))= ((z−3)/2) and the plane 3x+4y+z+5 = 0 |
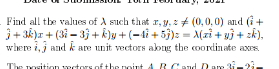
|

|