Question and Answers Forum
Question Number 8347 by sou1618 last updated on 09/Oct/16
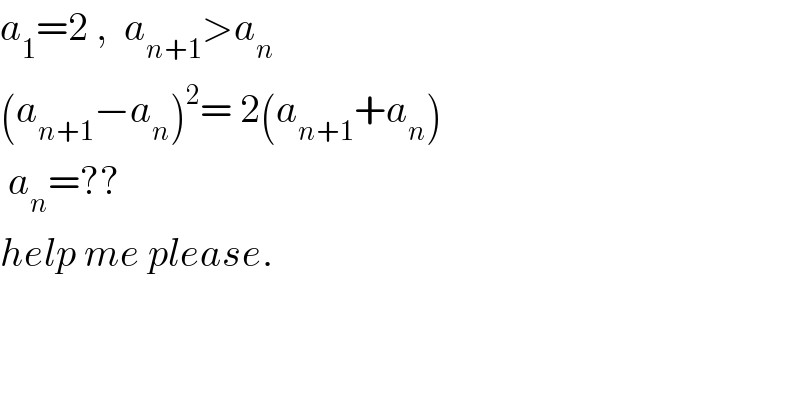
Commented by sou1618 last updated on 09/Oct/16
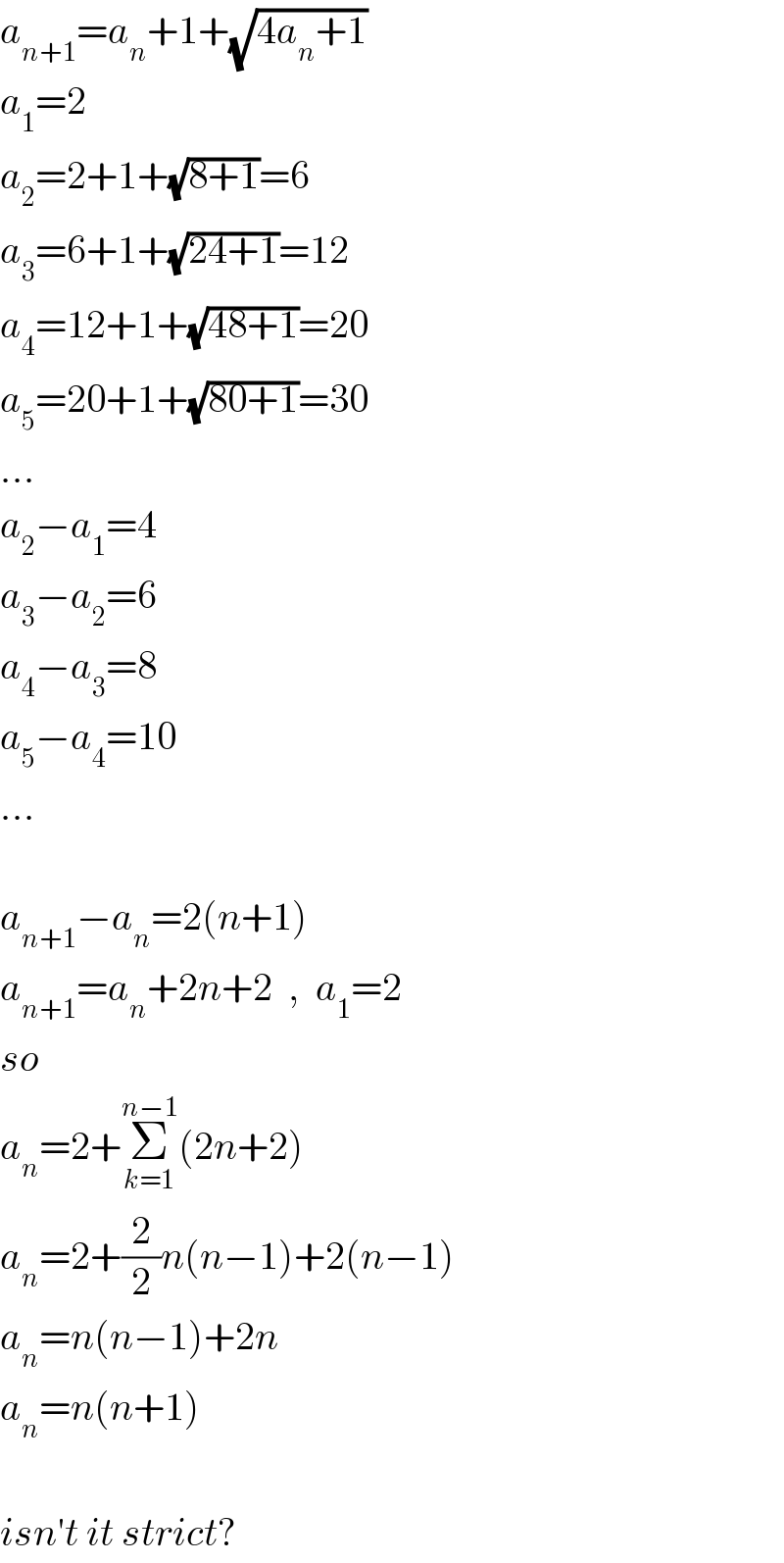
Commented by Rasheed Soomro last updated on 12/Oct/16
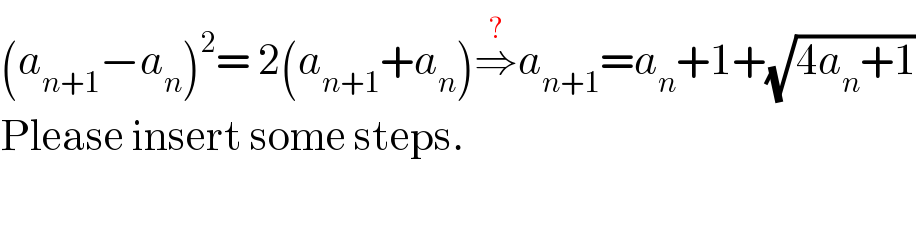
Commented by prakash jain last updated on 14/Oct/16
![(a_(n+1) −a_n )^2 −2(a_(n+1) −a_n )+1−4a_n −1=0 (a_(n+1) −a_n −1)^2 =4a_n +1 a_(n+1) =1+a_n +(√(4a_n +1)) If a_n is a polynomial then 4a_n +1 is a perfect square of polynomial. Let 4a_n +1=(c_0 +c_1 n+c_2 n^2 +c_3 n^3 +...+c_k n^k )^2 a_n =[(c_0 +c_1 n+c_2 n^2 +c_3 n^3 +...+c_k n^k )^2 −1]/4 a_(n+1) =[(c_0 +c_1 (n+1)+c_2 (n+1)^2 +c_3 (n+1)^3 +...)^2 −1]/4 Try for 4a_n +1=(c_0 +c_1 n+c_2 n^2 )^2 a_n =(1/4)[(c_0 +c_1 n+c_2 n^2 )^2 −1] Equating coeffcients n^4 : (1/4)c_2 ^2 =(1/4)c_2 ^2 n^3 :c_2 ^2 +(1/2)c_1 c_2 =(1/2)c_1 c_2 ⇒c_2 =0 No polynomial solution is possible if 4a_n +1 is a square of degree higher than 1. Degree 1 4a_n +1=(c_0 +c_1 n)^2 n^2 :(1/4)c_1 ^2 =(1/4)c_1 ^2 n: (1/2)c_1 c_0 +(1/2)c_1 ^2 =(1/2)c_1 c_0 +c_1 ⇒c_1 =2 n^0 :(c_0 ^2 /4)+((c_1 c_0 )/2)+(c_1 ^2 /4)−(1/4)=(c_0 ^2 /4)+c_0 +(3/4) ⇒c_0 +1−1/4=c_0 +3/4 a_n =((c_0 +2n)^2 −1)/4 a_1 =2⇒(c_0 +2)^2 −1=8 c_0 ^2 +4c_0 +4−1=8 c_0 ^2 +4c_0 −5=0 c_0 ^2 +5c_0 −c_0 −5=0 (c_0 −1)(c_0 +5)^2 =0 a_n = { ((((1+2n)^2 −1)/4=n^2 +n)),((((−5+2n)^2 −1)/4=n^2 −5n+6=(n−2)(n−3))) :} check (a_(n+1) −a_n )^2 =[(n−1)(n−2)−(n−2)(n−3)]^2 =4(n−2)^2 2(a_(n+1) +a_n )=2(n−2)(2n−4)=4(n−2)^2 comparing results determinant ((n,(n(n+1)),((n−2)(n−3))),(1,2,2),(2,6,0),(3,(12),0),(4,(20),2),(5,(30),6))](Q8509.png)
Commented by prakash jain last updated on 14/Oct/16
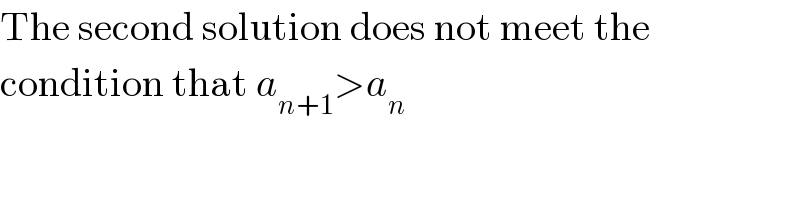
Commented by sou1618 last updated on 15/Oct/16