Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 98570 by HamraboyevFarruxjon last updated on 14/Jun/20

$$\mathit{a},\mathit{b},\mathit{c}>0\mathit{p}\mathit{r}\mathit{o}\mathit{v}\mathit{e}:$$$$\frac{\mathit{a}}{\sqrt{{\mathit{a}}^2+8\mathit{b}\mathit{c}}}+\frac{\mathit{b}}{\sqrt{{\mathit{b}}^2+8\mathit{a}\mathit{c}}}+\frac{\mathit{c}}{\sqrt{{\mathit{c}}^2+8\mathit{a}\mathit{b}}}⩾1$$$$\mathit{h}\mathit{e}\mathit{l}\mathit{p}\mathit{p}\mathit{l}\mathit{e}\mathit{a}\mathit{s}\mathit{e}...$$

Commented by MJS last updated on 14/Jun/20

$$\mathrm{extremes}\mathrm{where}a=b=c$$$$\mathrm{here}\mathrm{this}\mathrm{leads}\mathrm{to}$$$$3\frac{a}{\sqrt{a^2+8a^2}}=1\mathrm{for}a>0$$$$\Rightarrow \min \left(\mathrm{lhs}\right)=1\Rightarrow \mathrm{proven}$$

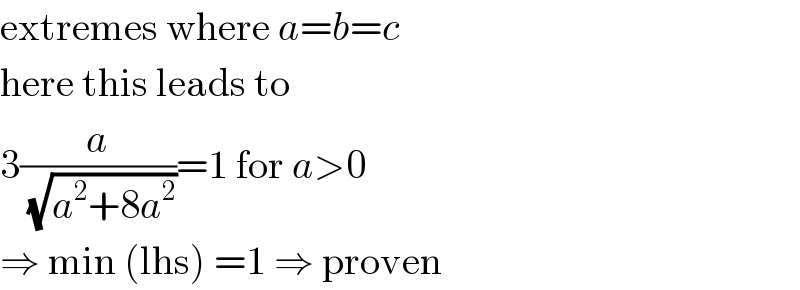
Answered by 1549442205 last updated on 15/Jun/20

$$$$$$$$$$\mathbf{Applying}\mathbf{the}\mathbf{Cauchi}-\mathbf{Schwartz}\mathbf{we}\mathbf{have}$$$$\mathrm{we}\mathrm{have}\mathrm{P}=\frac{\mathrm{a}}{\sqrt{{\mathrm{a}}^2+8\mathrm{bc}}}+\frac{\mathbf{b}}{\sqrt{{\mathbf{b}}^2+8\mathbf{ca}}}+\frac{\mathbf{c}}{\sqrt{{\mathbf{c}}^2+8\mathbf{ab}}}=\frac{{\mathbf{a}}^2}{\mathbf{a}\sqrt{{\mathbf{a}}^2+8\mathbf{bc}}}+\frac{{\mathbf{b}}^2}{\mathbf{b}\sqrt{{\mathbf{b}}^2+8\mathbf{ca}}}+\frac{{\mathbf{c}}^2}{\mathbf{c}\sqrt{{\mathbf{c}}^2+8\mathbf{ab}}}⩾\frac{{(\mathbf{a}+\mathbf{b}+\mathbf{c})}^2}{\mathbf{a}\sqrt{{\mathbf{a}}^2+8\mathbf{bc}}+\mathbf{b}\sqrt{{\mathbf{b}}^2+8\mathbf{ca}}+\mathbf{c}\sqrt{{\mathbf{c}}^2+8\mathbf{ab}}}$$$$\mathbf{On}\mathbf{the}\mathbf{other}\mathbf{hands},\mathbf{also}\mathbf{by}\mathbf{C}-\mathbf{S}\mathbf{we}\mathbf{have}$$$$\mathbf{a}\sqrt{{\mathbf{a}}^2+8\mathbf{bc}}+\mathbf{b}\sqrt{{\mathbf{b}}^2+8\mathbf{ca}}+\mathbf{c}\sqrt{{\mathbf{c}}^2+8\mathbf{ab}}=\sqrt{\mathbf{a}}.\sqrt{{\mathbf{a}}^3+8\mathbf{abc}}+\sqrt{\mathbf{b}}.\sqrt{{\mathbf{b}}^3+8\mathbf{abc}}+\sqrt{\mathbf{c}}.\sqrt{{\mathbf{c}}^3+8\mathbf{abc}}$$$$⩽\sqrt{(\mathbf{a}+\mathbf{b}+\mathbf{c})({\mathbf{a}}^3+{\mathbf{b}}^3+{\mathbf{c}}^3+24\mathbf{abc})}.\mathbf{Hence},$$$$\mathbf{P}⩾\frac{{(\mathbf{a}+\mathbf{b}+\mathbf{c})}^2}{\sqrt{(\mathbf{a}+\mathbf{b}+\mathbf{c})({\mathbf{a}}^3+{\mathbf{b}}^3+{\mathbf{c}}^3+24\mathbf{abc})}}=\sqrt{\frac{{(\mathbf{a}+\mathbf{b}+\mathbf{c})}^3}{{\mathbf{a}}^3+{\mathbf{b}}^3+{\mathbf{c}}^3+24\mathbf{abc}}}.\mathbf{Therefore},\mathbf{it}\mathbf{is}\mathbf{enough}$$$$\mathbf{to}\mathbf{prove}\mathbf{that}\frac{{(\mathbf{a}+\mathbf{b}+\mathbf{c})}^3}{{\mathbf{a}}^3+{\mathbf{b}}^3+{\mathbf{c}}^3+24\mathbf{abc}}⩾1\iff$$$${(\mathbf{a}+\mathbf{b}+\mathbf{c})}^3⩾{\mathbf{a}}^3+{\mathbf{b}}^3+{\mathbf{c}}^3+24\mathbf{abc}\iff (\mathbf{a}+\mathbf{b})(\mathbf{b}+\mathbf{c})(\mathbf{c}+\mathbf{a})⩾8\mathbf{abc}$$$$\mathbf{This}\mathbf{final}\mathbf{inequality}\mathbf{is}\mathbf{always}\mathbf{true}\mathbf{because}$$$$\mathbf{it}\mathbf{is}\mathbf{followed}\mathbf{from}\mathbf{the}\mathbf{inequlities}:$$$$\mathbf{a}+\mathbf{b}⩾2\sqrt{\mathbf{ab}},\mathbf{b}+\mathbf{c}⩾2\sqrt{\mathbf{bc}},\mathbf{c}+\mathbf{a}⩾2\sqrt{\mathbf{ca}}$$$$\mathbf{Thus},\mathbf{P}⩾1.\mathbf{The}\mathbf{equality}\mathbf{occurs}\mathbf{if}\mathbf{an}\mathbf{only}\mathbf{if}$$$$\mathbf{a}=\mathbf{b}=\mathbf{c}(\mathbf{q}.\mathbf{e}.\mathbf{d})$$

Commented by Farruxjano last updated on 15/Jun/20

$$\mathrm{Sir}\mathrm{thanks}\mathrm{a}\mathrm{lot}$$

Commented by 1549442205 last updated on 25/Jun/20

$$\mathrm{Thank}\mathrm{you}!\mathrm{you}\mathrm{are}\mathrm{wellcome},\mathrm{sir}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com