
Question and Answers Forum
Question Number 133228 by mnjuly1970 last updated on 20/Feb/21
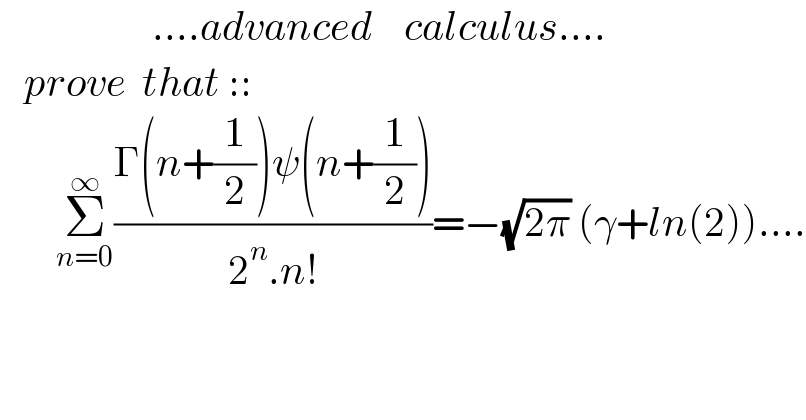
Answered by Dwaipayan Shikari last updated on 20/Feb/21
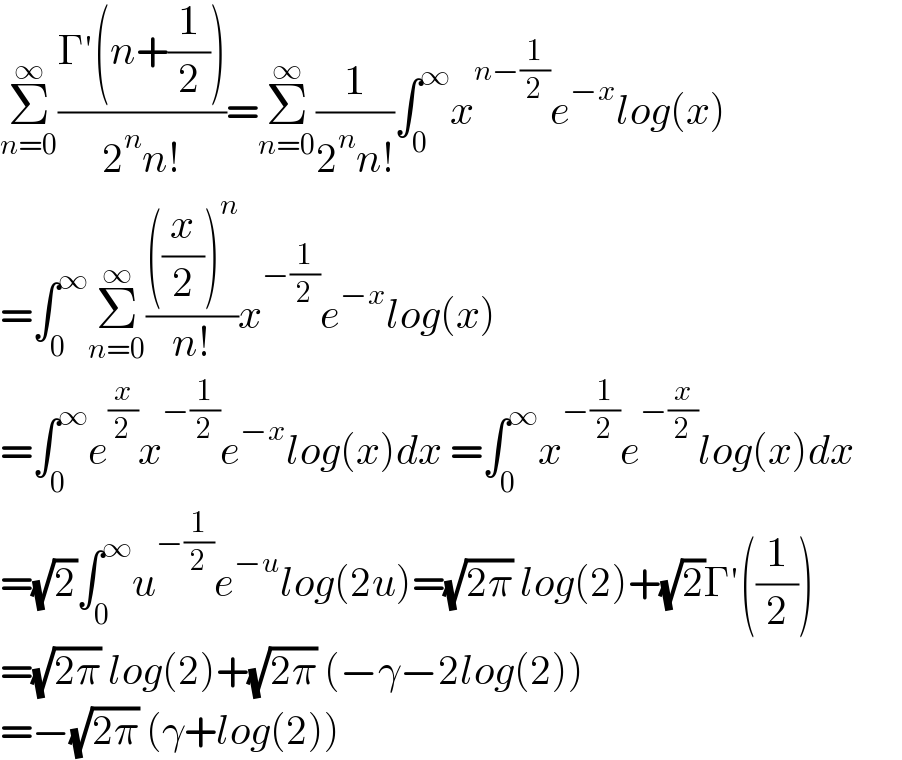
Commented by mnjuly1970 last updated on 20/Feb/21

| ||
Question and Answers Forum | ||
Question Number 133228 by mnjuly1970 last updated on 20/Feb/21 | ||
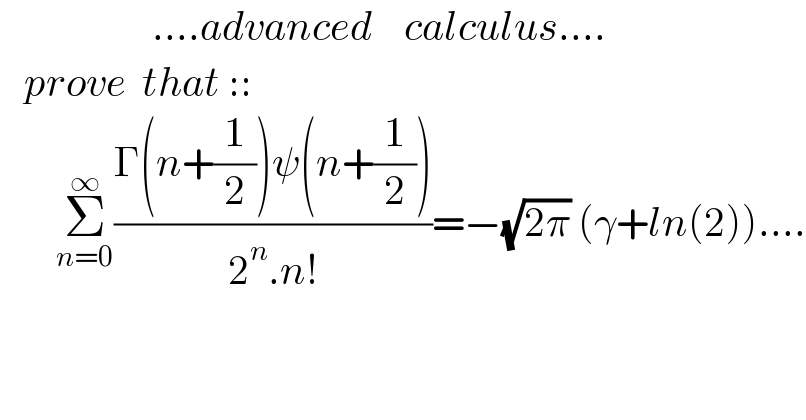 | ||
Answered by Dwaipayan Shikari last updated on 20/Feb/21 | ||
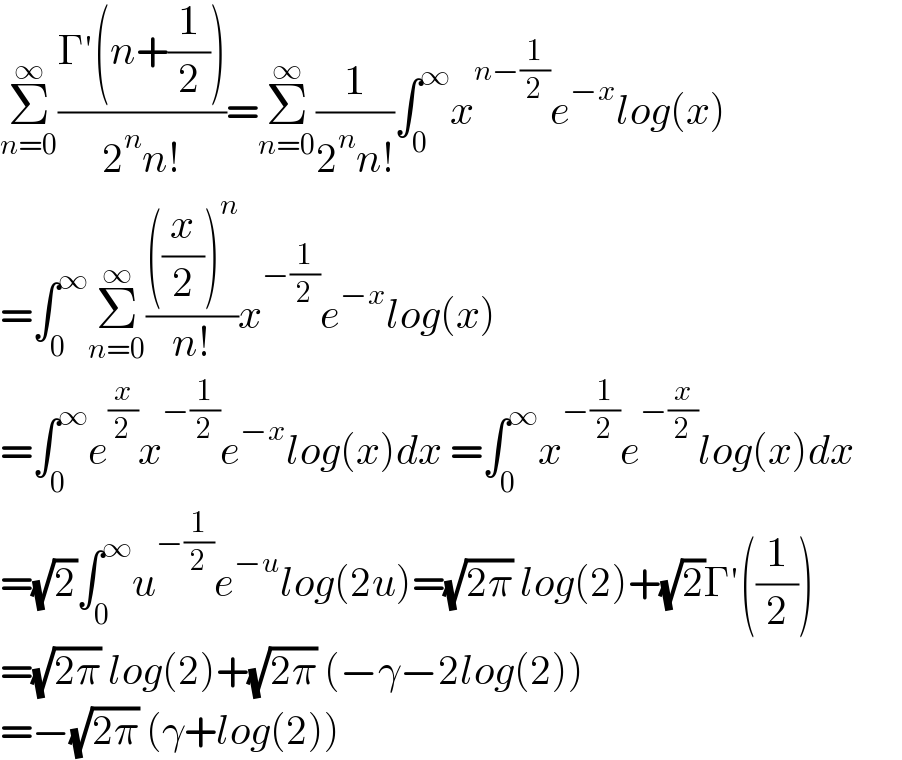 | ||
| ||
Commented by mnjuly1970 last updated on 20/Feb/21 | ||
 | ||