@bemath@ ∫_0 ^2 x ((8−x^3 ))^(1/3) dx =?


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 107184 by bemath last updated on 09/Aug/20

$@ b e m a t h @$ $\underset{0}{\int^{2}} x \sqrt[3]{8 - x^{3}} d x = ?$
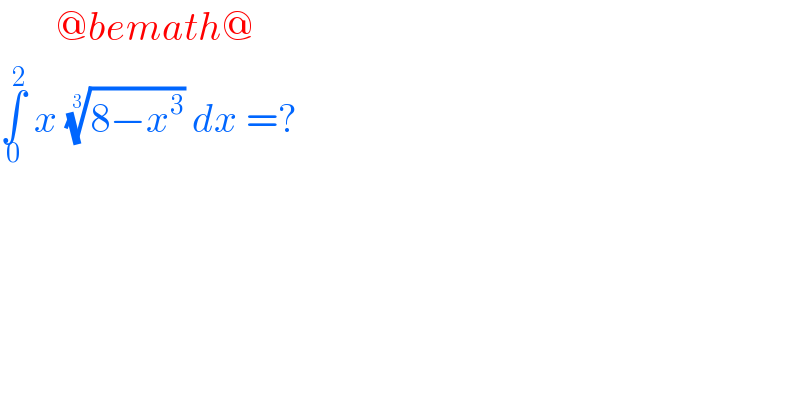
	Answered by john santu last updated on 09/Aug/20

	Commented by john santu last updated on 09/Aug/20

	$typo 8 v = x^{3}$
	Commented by bobhans last updated on 09/Aug/20

	$typo the last line : \frac{16 π}{9 \sqrt{3}}$
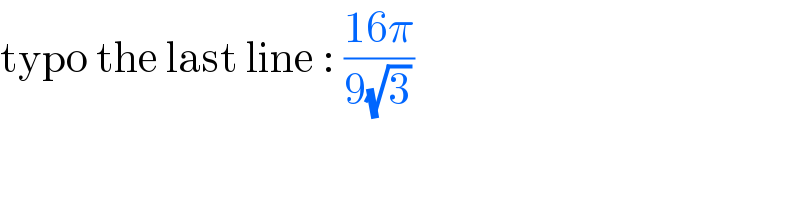
	Commented by john santu last updated on 09/Aug/20

	$haha . . . thanks$
	Answered by 1549442205PVT last updated on 12/Aug/20
	$Set (8/x^3 )−1=t^3 ⇒3t^2 dt=−((24)/x^4 )dx ⇒^3 (√(8−x^3 )) =xt,dx=−((x^4 t^2 dt)/8) ⇒F=∫((x^2 t.x^4 t^2 )/(−8))dt=−(1/8)∫ t^3 x^6 dt =((−1)/8)∫t^3 .((8/(1+t^3 )))^2 dt=−8∫(t^3 /((1+t^3 )^2 ))dt =−8∫((t^3 +1−1)/((1+t^3 )^2 ))dt=−8∫(dt/(1+t^3 ))−8∫(dt/((1+t^3 )^2 )) (1/(1+t^3 ))=(a/(1+t))+((bt+c)/(t^2 −t+1))⇔(((a+b)t^2 +(b+c−a)t+a+c)/((1+t)(t^2 −t+1)))=(1/(t^3 +1)) ⇔ { ((a+b=0)),((b+c−a=0)),((a+c=1)) :} ⇔ { ((a=1/3)),((b=−1/3)),((c=2/3)) :} A=∫(dt/(1+t^3 ))=∫(dt/(3(1+t)))−∫(((t−2)dt)/(3(t^2 −t+1))) =(1/3)lnt−(1/6)∫((2t−1−3)/((t^2 −t+1)))dt=(1/3)lnt −(1/6)∫((d(t^2 −t+1))/(t^2 −t+1))+(1/2)∫(dt/((t−(1/2))^2 +(((√3)/2))^2 )) =(1/3)lnt−(1/6)ln(t^2 −t+1)+(1/2)×(2/( (√3)))tan^(−1) (((2x−1)/( (√3)))) B=(1/((1+t^3 )^2 ))=[(1/3)((1/(t+1))−((t−2)/(t^2 −t+1)))]^2 9B=(1/((1+t)^2 ))−((t^2 −4t+4)/((t^2 −t+1)^2 ))−((2(t−2))/((t+1)(t^2 −t+1))) =(1/((1+t)^2 ))−((t^2 −t+1−3t+3)/((t^2 −t+1)^2 ))−(2/(t^2 −t+1))+2((1/(t+1))−((t−2)/(t^2 −t+1))) =(1/((1+t)^2 ))−(1/(t^2 −t+1))+((3(t−1))/((t^2 −t+1)^2 ))−(2/(t^2 −t+1))+(2/(t+1))−((2(t−2))/(t^2 −t+1)) =(1/((t+1)^2 ))+(2/(t+1))+((3(t−1))/((t^2 −t+1)^2 ))−((2t−1)/(t^2 −t+1)) ∫(dt/((1+t^3 )^2 ))=∫((1/((t+1)^2 ))+(2/(t+1))+((3(t−1))/((t^2 −t+1)^2 ))−((2t−1)/(t^2 −t+1)))dt =∫((d(t+1))/((t+1)^2 ))+2∫((d(t+1))/(t+1))+(3/2)∫((2t−1)/((t^2 −t+1)^2 ))dt−(3/2)∫(dt/((t^2 −t+1)^2 ))−∫ ((d(t^2 −t+1))/(t^2 −t+1)) =−(1/(t+1))+2ln(t+1)−(3/(2(t^2 −t+1)))−ln(t^2 −t+1)−(3/(2(t^2 −t+1)^2 )) I_2 =∫(dt/((t^2 −t+1)^2 ))=∫((d(t−(1/2)))/([(t−(1/2))^2 +(((√3)/2))^2 ]^2 )).Set u=t−(1/2),a=((√3)/2) I_2 =∫(du/((u^2 +a)^2 ))=(1/(2a^2 (2−1))).(u/((u^2 +a^2 )^(2−1) ))+(1/a^2 ).((2.2−3)/(2.2−2)).I_1 =(2/3).(u/((u^2 +a^2 )))+(4/3).(1/2)∫(du/(u^2 +a^2 )) =(2/3).((t−(1/2))/((t^2 −t+1)))+(2/3).(2/( (√3)))tan^(−1) (((2t−1)/( (√3)))) =((2t−1)/(3(t^2 −t+1)))+(4/(3(√3)))tan^(−1) (((2t−1)/( (√3)))) Hence, 9B=((−1)/(t+1))+2ln(t+1)−(3/(2(t^2 −t+1)))−ln(t^2 −t+1)−(3/(2(t^2 −t+1)^2 )) =((−1)/(t+1))−(3/(2(t^2 −t+1)))+2ln((t+1)/(t^2 −t+1))−3I_2 =((−1)/(t+1))−(3/(2(t^2 −t+1)))+2ln((t+1)/(t^2 −t+1))−((2t−1)/(t^2 −t+1))−(4/( (√3)))tan^(−1) (((2t−1)/( (√3)))) F=−8A−8B=−8[(1/3)lnt−(1/6)ln(t^2 −t+1)+(1/2)×(2/( (√3)))tan^(−1) (((2x−1)/( (√3))))] −(8/9)[=((−1)/(t+1))−(3/(2(t^2 −t+1)))+2ln((t+1)/(t^2 −t+1))−((2t−1)/(t^2 −t+1))−(4/( (√3)))tan^(−1) (((2t−1)/( (√3))))]$
	$Set \frac{8}{x^{3}} - 1 = t^{3} \Rightarrow {3 t}^{2} dt = - \frac{24}{x^{4}} dx$ $\Rightarrow^{3} \sqrt{8 - x^{3}} = xt, dx = - \frac{x^{4} t^{2} dt}{8}$ $\Rightarrow F = \int \frac{x^{2} t . x^{4} t^{2}}{- 8} dt = - \frac{1}{8} \int t^{3} x^{6} dt$ $= \frac{- 1}{8} \int t^{3} . {(\frac{8}{1 + t^{3}})}^{2} dt = - 8 \int \frac{t^{3}}{{(1 + t^{3})}^{2}} dt$ $= - 8 \int \frac{t^{3} + 1 - 1}{{(1 + t^{3})}^{2}} dt = - 8 \int \frac{dt}{1 + t^{3}} - 8 \int \frac{dt}{{(1 + t^{3})}^{2}}$ $\frac{1}{1 + t^{3}} = \frac{a}{1 + t} + \frac{bt + c}{t^{2} - t + 1} \Leftrightarrow \frac{(a + b) t^{2} + (b + c - a) t + a + c}{(1 + t) (t^{2} - t + 1)} = \frac{1}{t^{3} + 1}$ $\Leftrightarrow {\begin{cases} a + b = 0 \\ b + c - a = 0 \\ a + c = 1 \end{cases} \Leftrightarrow {\begin{cases} a = 1 / 3 \\ b = - 1 / 3 \\ c = 2 / 3 \end{cases}$ $A = \int \frac{dt}{1 + t^{3}} = \int \frac{dt}{3 (1 + t)} - \int \frac{(t - 2) dt}{3 (t^{2} - t + 1)}$ $= \frac{1}{3} lnt - \frac{1}{6} \int \frac{2 t - 1 - 3}{(t^{2} - t + 1)} dt = \frac{1}{3} lnt$ $- \frac{1}{6} \int \frac{d (t^{2} - t + 1)}{t^{2} - t + 1} + \frac{1}{2} \int \frac{dt}{{(t - \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}}$ $= \frac{1}{3} lnt - \frac{1}{6} \ln (t^{2} - t + 1) + \frac{1}{2} \times \frac{2}{\sqrt{3}} \tan^{- 1} (\frac{2 x - 1}{\sqrt{3}})$ $B = \frac{1}{{(1 + t^{3})}^{2}} = {[\frac{1}{3} (\frac{1}{t + 1} - \frac{t - 2}{t^{2} - t + 1})]}^{2}$ $9 B = \frac{1}{{(1 + t)}^{2}} - \frac{t^{2} - 4 t + 4}{{(t^{2} - t + 1)}^{2}} - \frac{2 (t - 2)}{(t + 1) (t^{2} - t + 1)}$ $= \frac{1}{{(1 + t)}^{2}} - \frac{t^{2} - t + 1 - 3 t + 3}{{(t^{2} - t + 1)}^{2}} - \frac{2}{t^{2} - t + 1} + 2 (\frac{1}{t + 1} - \frac{t - 2}{t^{2} - t + 1})$ $= \frac{1}{{(1 + t)}^{2}} - \frac{1}{t^{2} - t + 1} + \frac{3 (t - 1)}{{(t^{2} - t + 1)}^{2}} - \frac{2}{t^{2} - t + 1} + \frac{2}{t + 1} - \frac{2 (t - 2)}{t^{2} - t + 1}$ $= \frac{1}{{(t + 1)}^{2}} + \frac{2}{t + 1} + \frac{3 (t - 1)}{{(t^{2} - t + 1)}^{2}} - \frac{2 t - 1}{t^{2} - t + 1}$ $\int \frac{dt}{{(1 + t^{3})}^{2}} = \int (\frac{1}{{(t + 1)}^{2}} + \frac{2}{t + 1} + \frac{3 (t - 1)}{{(t^{2} - t + 1)}^{2}} - \frac{2 t - 1}{t^{2} - t + 1}) dt$ $= \int \frac{d (t + 1)}{{(t + 1)}^{2}} + 2 \int \frac{d (t + 1)}{t + 1} + \frac{3}{2} \int \frac{2 t - 1}{{(t^{2} - t + 1)}^{2}} dt - \frac{3}{2} \int \frac{dt}{{(t^{2} - t + 1)}^{2}} - \int \frac{d (t^{2} - t + 1)}{t^{2} - t + 1}$ $= - \frac{1}{t + 1} + 2 \ln (t + 1) - \frac{3}{2 (t^{2} - t + 1)} - \ln (t^{2} - t + 1) - \frac{3}{2 {(t^{2} - t + 1)}^{2}}$ $I_{2} = \int \frac{dt}{{(t^{2} - t + 1)}^{2}} = \int \frac{d (t - \frac{1}{2})}{{[{(t - \frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}]}^{2}} . Set u = t - \frac{1}{2}, a = \frac{\sqrt{3}}{2}$ $I_{2} = \int \frac{du}{{(u^{2} + a)}^{2}} = \frac{1}{{2 a}^{2} (2 - 1)} . \frac{u}{{(u^{2} + a^{2})}^{2 - 1}} + \frac{1}{a^{2}} . \frac{2.2 - 3}{2.2 - 2} . I_{1}$ $= \frac{2}{3} . \frac{u}{(u^{2} + a^{2})} + \frac{4}{3} . \frac{1}{2} \int \frac{du}{u^{2} + a^{2}}$ $= \frac{2}{3} . \frac{t - \frac{1}{2}}{(t^{2} - t + 1)} + \frac{2}{3} . \frac{2}{\sqrt{3}} \tan^{- 1} (\frac{2 t - 1}{\sqrt{3}})$ $= \frac{2 t - 1}{3 (t^{2} - t + 1)} + \frac{4}{3 \sqrt{3}} \tan^{- 1} (\frac{2 t - 1}{\sqrt{3}})$ $Hence,$ $9 B = \frac{- 1}{t + 1} + 2 \ln (t + 1) - \frac{3}{2 (t^{2} - t + 1)} - \ln (t^{2} - t + 1) - \frac{3}{2 {(t^{2} - t + 1)}^{2}}$ $= \frac{- 1}{t + 1} - \frac{3}{2 (t^{2} - t + 1)} + 2 \ln \frac{t + 1}{t^{2} - t + 1} - {3 I}_{2}$ $= \frac{- 1}{t + 1} - \frac{3}{2 (t^{2} - t + 1)} + 2 \ln \frac{t + 1}{t^{2} - t + 1} - \frac{2 t - 1}{t^{2} - t + 1} - \frac{4}{\sqrt{3}} \tan^{- 1} (\frac{2 t - 1}{\sqrt{3}})$ $F = - 8 A - 8 B = - 8 [\frac{1}{3} lnt - \frac{1}{6} \ln (t^{2} - t + 1) + \frac{1}{2} \times \frac{2}{\sqrt{3}} \tan^{- 1} (\frac{2 x - 1}{\sqrt{3}})]$ $- \frac{8}{9} [= \frac{- 1}{t + 1} - \frac{3}{2 (t^{2} - t + 1)} + 2 \ln \frac{t + 1}{t^{2} - t + 1} - \frac{2 t - 1}{t^{2} - t + 1} - \frac{4}{\sqrt{3}} \tan^{- 1} (\frac{2 t - 1}{\sqrt{3}})]$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum