
Question and Answers Forum
Question Number 26055 by abdo imad last updated on 18/Dec/17
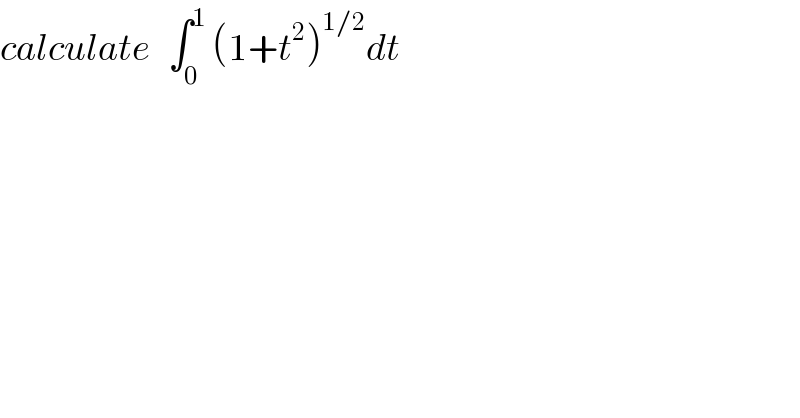
Answered by Joel578 last updated on 19/Dec/17
![I = ∫_0 ^1 (√(t^2 + 1)) dt Let t = tan x → dt = sec^2 x dx t = 0 → x = 0 t = 1 → x = (π/4) I = ∫_0 ^(π/4) (√(tan^2 x + 1)) . sec^2 x dx = ∫_0 ^(π/4) sec^3 x dx Using IBP give: = [(1/2)(sec x tan x) − (1/2)ln ∣sec x + tan x∣]_0 ^(π/4) = [((√2)/2) − (1/2)ln ((√2) + 1)] − [− (1/2)ln (1)] = ((√2)/2) − (1/2)ln ((√2) + 1)](Q26066.png)
| ||
Question and Answers Forum | ||
Question Number 26055 by abdo imad last updated on 18/Dec/17 | ||
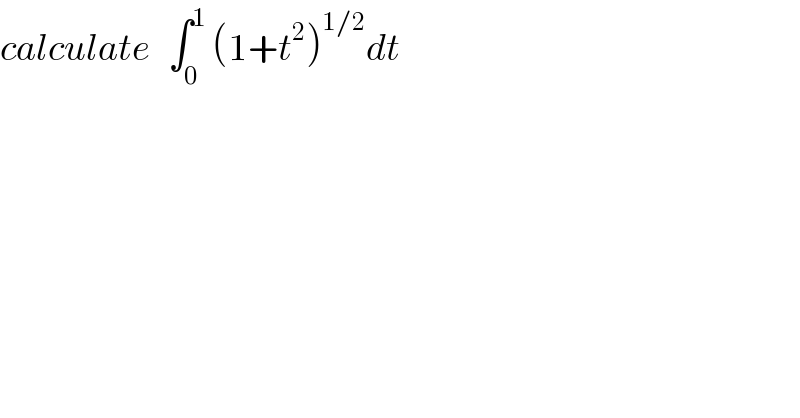 | ||
Answered by Joel578 last updated on 19/Dec/17 | ||
![I = ∫_0 ^1 (√(t^2 + 1)) dt Let t = tan x → dt = sec^2 x dx t = 0 → x = 0 t = 1 → x = (π/4) I = ∫_0 ^(π/4) (√(tan^2 x + 1)) . sec^2 x dx = ∫_0 ^(π/4) sec^3 x dx Using IBP give: = [(1/2)(sec x tan x) − (1/2)ln ∣sec x + tan x∣]_0 ^(π/4) = [((√2)/2) − (1/2)ln ((√2) + 1)] − [− (1/2)ln (1)] = ((√2)/2) − (1/2)ln ((√2) + 1)](Q26066.png) | ||
| ||