
Question and Answers Forum
Question Number 33984 by abdo imad last updated on 28/Apr/18
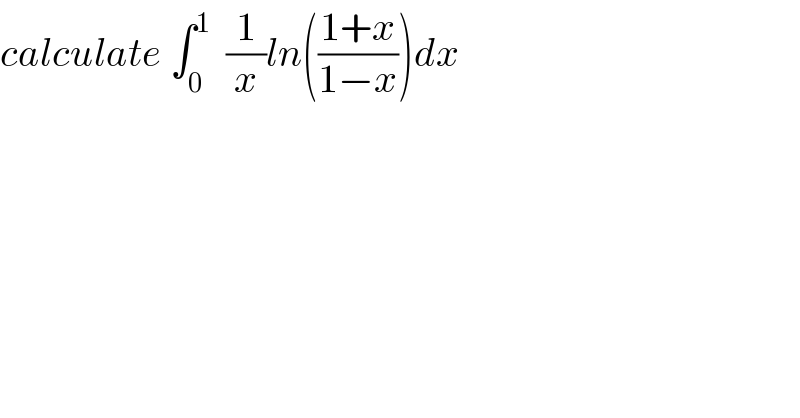
Commented by prof Abdo imad last updated on 29/Apr/18
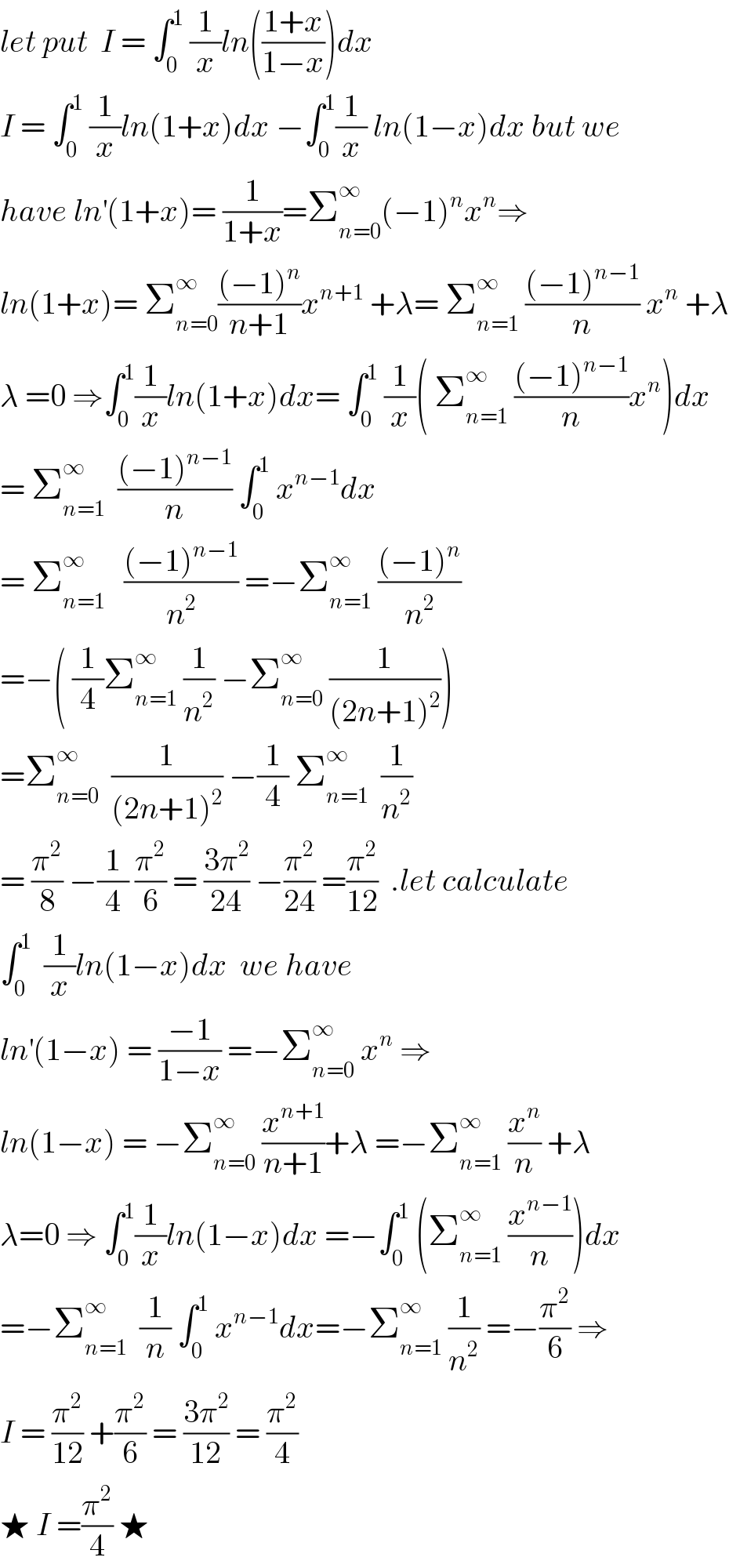
Answered by hknkrc46 last updated on 29/Apr/18
![ln (((1+x)/(1−x)))=ln ((((1+x)(1+x))/((1−x)(1+x))))=ln ((((1+x)^2 )/(1−x^2 ))) =ln (((1+x)/(√(1−x^2 ))))^2 =2ln ((1+x)/(√(1−x^2 ))) ∫(1/x)ln (((1+x)/(1−x)))dx=2∫((1+x)/(x(√(1−x^2 ))))dx→ { ((x=cos 2ψ⇒dx=−2sin2 ψdψ)),((x→0,ψ→(π/4)∧x→1,ψ→0)) :} −2∫(((1+cos 2ψ)sin 2ψ)/(cos 2ψ(√(1−cos^2 2ψ))))dψ=−2∫((2cos^2 ψsin 2ψ)/(cos 2ψsin 2ψ))dψ =−4∫((cos^2 ψ)/(cos 2ψ))dψ=−4∫((1−sin^2 ψ)/(cos 2ψ))dψ =−4∫sec 2ψdψ+4∫((sin^2 ψ)/(cos 2ψ))dψ =−4∫sec 2ψdψ+4∫(((1−cos 2ψ)/2)/(cos 2ψ))dψ =−4∫sec 2ψdψ+2∫sec 2ψdψ−2∫dψ =−2∫sec 2ψdψ−2∫dψ=−2∫(dψ/(cos 2ψ))−2∫dψ =−2∫(dψ/(cos 2ψ))−2∫dψ=−ln ∣sec 2ψ+tan 2ψ∣−2ψ+C ∫_0 ^1 (1/x)ln(((1+x)/(1−x)))dx=[−ln ∣sec 2ψ+tan 2ψ∣−2ψ]_(π/4) ^0 =−∞](Q34034.png)
| ||
Question and Answers Forum | ||
Question Number 33984 by abdo imad last updated on 28/Apr/18 | ||
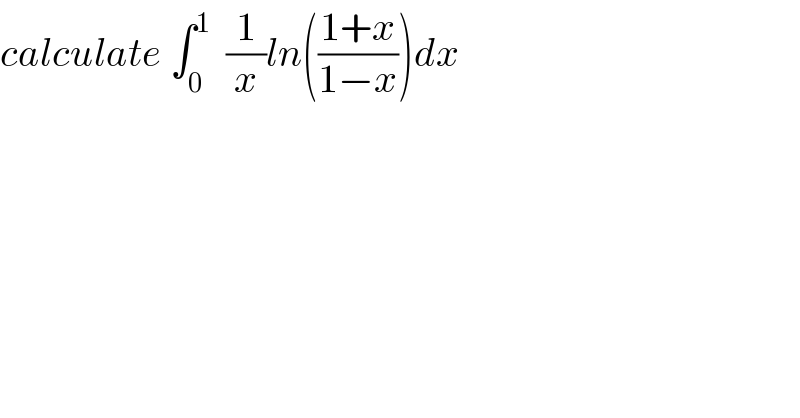 | ||
Commented by prof Abdo imad last updated on 29/Apr/18 | ||
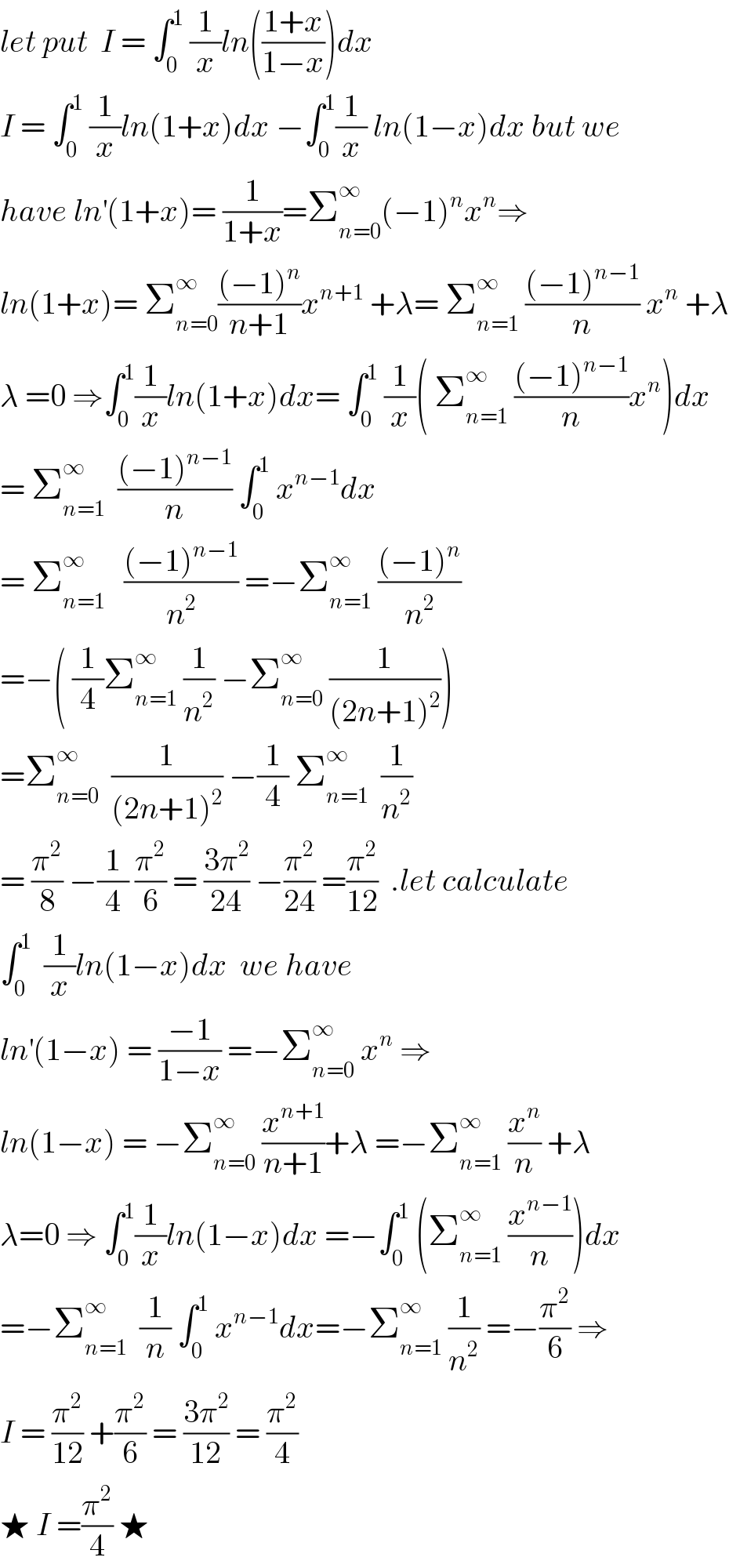 | ||
Answered by hknkrc46 last updated on 29/Apr/18 | ||
![ln (((1+x)/(1−x)))=ln ((((1+x)(1+x))/((1−x)(1+x))))=ln ((((1+x)^2 )/(1−x^2 ))) =ln (((1+x)/(√(1−x^2 ))))^2 =2ln ((1+x)/(√(1−x^2 ))) ∫(1/x)ln (((1+x)/(1−x)))dx=2∫((1+x)/(x(√(1−x^2 ))))dx→ { ((x=cos 2ψ⇒dx=−2sin2 ψdψ)),((x→0,ψ→(π/4)∧x→1,ψ→0)) :} −2∫(((1+cos 2ψ)sin 2ψ)/(cos 2ψ(√(1−cos^2 2ψ))))dψ=−2∫((2cos^2 ψsin 2ψ)/(cos 2ψsin 2ψ))dψ =−4∫((cos^2 ψ)/(cos 2ψ))dψ=−4∫((1−sin^2 ψ)/(cos 2ψ))dψ =−4∫sec 2ψdψ+4∫((sin^2 ψ)/(cos 2ψ))dψ =−4∫sec 2ψdψ+4∫(((1−cos 2ψ)/2)/(cos 2ψ))dψ =−4∫sec 2ψdψ+2∫sec 2ψdψ−2∫dψ =−2∫sec 2ψdψ−2∫dψ=−2∫(dψ/(cos 2ψ))−2∫dψ =−2∫(dψ/(cos 2ψ))−2∫dψ=−ln ∣sec 2ψ+tan 2ψ∣−2ψ+C ∫_0 ^1 (1/x)ln(((1+x)/(1−x)))dx=[−ln ∣sec 2ψ+tan 2ψ∣−2ψ]_(π/4) ^0 =−∞](Q34034.png) | ||
| ||