
Question and Answers Forum
Question Number 40887 by prof Abdo imad last updated on 28/Jul/18
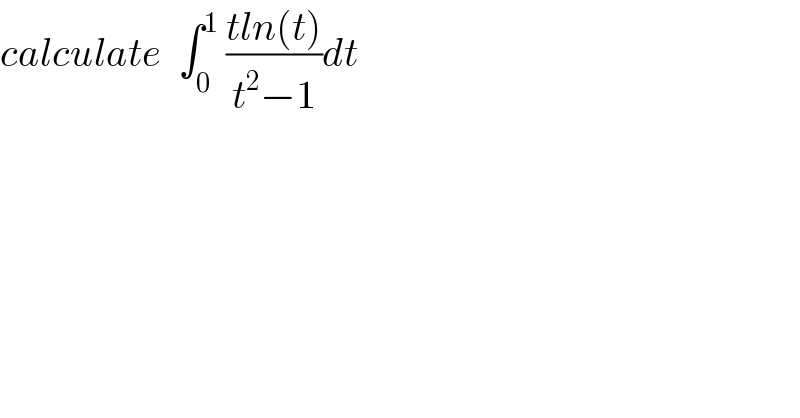
Commented by prof Abdo imad last updated on 30/Jul/18
![let I = ∫_0 ^1 ((tln(t))/(t^2 −1))dt I =−∫_0 ^1 tln(t)(Σ_(n=0) ^∞ t^(2n) )dt =−Σ_(n=0) ^∞ ∫_0 ^1 t^(2n+1) ln(t)dt by parts A_n =∫_0 ^1 t^(2n+1) ln(t)dt =[(1/(2n+2))t^(2n+2) ln(t)]_0 ^1 −∫_0 ^1 (1/(2n+2)) t^(2n+1) dt =−(1/((2n+2)^2 )) ⇒ I =Σ_(n=0) ^∞ (1/((2n+2)^2 )) =(1/4) Σ_(n=0) ^∞ (1/((n+1)^2 )) =(1/4)Σ_(n=1) ^∞ (1/n^2 ) =(1/4) .(π^2 /6) ⇒ I =(π^2 /(24))](Q40978.png)
| ||
Question and Answers Forum | ||
Question Number 40887 by prof Abdo imad last updated on 28/Jul/18 | ||
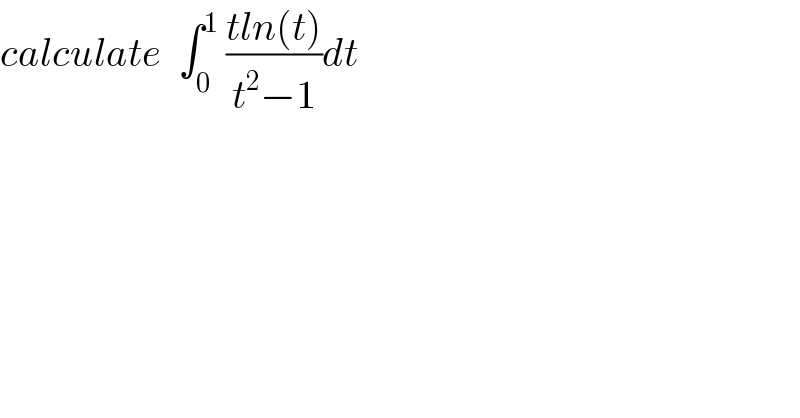 | ||
Commented by prof Abdo imad last updated on 30/Jul/18 | ||
![let I = ∫_0 ^1 ((tln(t))/(t^2 −1))dt I =−∫_0 ^1 tln(t)(Σ_(n=0) ^∞ t^(2n) )dt =−Σ_(n=0) ^∞ ∫_0 ^1 t^(2n+1) ln(t)dt by parts A_n =∫_0 ^1 t^(2n+1) ln(t)dt =[(1/(2n+2))t^(2n+2) ln(t)]_0 ^1 −∫_0 ^1 (1/(2n+2)) t^(2n+1) dt =−(1/((2n+2)^2 )) ⇒ I =Σ_(n=0) ^∞ (1/((2n+2)^2 )) =(1/4) Σ_(n=0) ^∞ (1/((n+1)^2 )) =(1/4)Σ_(n=1) ^∞ (1/n^2 ) =(1/4) .(π^2 /6) ⇒ I =(π^2 /(24))](Q40978.png) | ||