Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 37893 by abdo mathsup 649 cc last updated on 19/Jun/18

$$calculate{\int }_0^1\sqrt{x+\sqrt{x+1}}dx.$$

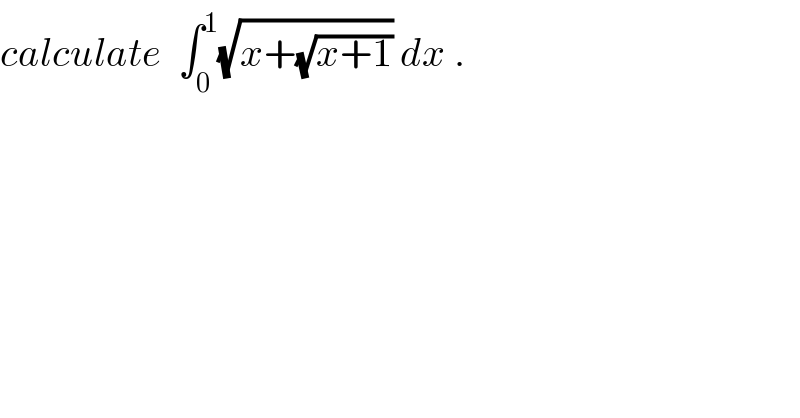
Commented by math khazana by abdo last updated on 21/Jun/18

$$let\sqrt{x+\sqrt{x+1}}=t\Rightarrow x+\sqrt{x+1}=t^2\Rightarrow$$$$\sqrt{x+1}=t^2-x\Rightarrow x+1={(t^2-x)}^2\Rightarrow$$$$x=t^4-2{xt}^2+x^2-1\Rightarrow x^2-(2t^2+1)x+t^4-1=0\Rightarrow$$$$\mathrm{\Delta }={(2t^2+1)}^2-4(t^4-1)$$$$=4t^4+4t^2+1-4t^4+4=4t^2+5\Rightarrow$$$$x_1=\frac{2t^2+1+\sqrt{4t^2+5}}{2}$$$$x_2=\frac{2t^2+1-\sqrt{4t^2+5}}{2}withconditiont⩾0andx⩾-1$$$$and{t}^2-x⩾0$$$$t^2-x_2=t^2-\frac{2t^2+1-\sqrt{4t^2+5}}{2}$$$$=\frac{-1+\sqrt{4t^2+5}}{2}⩾0$$$$x_2+1=\frac{2t^2+1-\sqrt{4t^2+5}}{2}+1$$$$=\frac{2t^2+3-\sqrt{4t^2+5}}{2}⩾0sowetake$$$$x=\frac{2t^2+1-\sqrt{4t^2+5}}{2}\Rightarrow \frac{dx}{dt}=2t-\frac{1}{2}\frac{8t}{2\sqrt{4t^2+5}}$$$$=2t-\frac{2t}{\sqrt{4t^2+5}}\Rightarrow$$$${\int }_0^1\sqrt{x+\sqrt{x+1}}dx={\int }_1^{\sqrt{1+\sqrt{2}}}t(2t-\frac{2t}{\sqrt{4t^2+5}})dt$$$$=2{\int }_1^{\sqrt{1+\sqrt{2}}}{t}^{2}dt-2{\int }_1^{\sqrt{1+\sqrt{2}}}\frac{t^2}{\sqrt{4t^2+5}}dt$$$$=2{\left[\frac{t^3}{3}\right]}_1^{\sqrt{1+\sqrt{2}}}-\frac{1}{2}{\int }_1^{\sqrt{1+\sqrt{2}}}\frac{4t^2+5-5}{\sqrt{4t^2+5}}dt$$$$=2((1+\sqrt{2})\sqrt{1+\sqrt{2}}-\frac{1}{3})-\frac{1}{2}{\int }_1^{\sqrt{1+\sqrt{2}}}\sqrt{4t^2+5}dt$$$$+\frac{5}{2}{\int }_1^{\sqrt{1+\sqrt{2}}}\frac{dt}{\sqrt{4t^2+5}}changement$$$$2t=\sqrt{5}sh\left(x\right)give$$$${\int }_1^{\sqrt{1+\sqrt{2}}}\sqrt{4t^2+5}dt={\int }_{argsh\left(\frac{2}{\sqrt{5}}\right)}^{arsh\left(\frac{2}{\sqrt{5}}\sqrt{1+\sqrt{2}}\right)}\sqrt{5}ch\left(x\right)\frac{\sqrt{5}}{2}chxdx$$$$=\frac{5}{2}{\int }_{\alpha }^{\beta }\frac{1+ch\left(2x\right)}{2}dx=\frac{5}{4}(\beta -\alpha )+\frac{5}{8}{\left[sh\left(2x\right)\right]}_{\alpha }^{\beta }$$$$=\frac{5}{4}(\beta -\alpha )+\frac{5}{8}(sh\left(2\beta \right)-sh\left(2\alpha \right))....$$

Answered by MJS last updated on 19/Jun/18

$$\int \sqrt{x+\sqrt{x+1}}dx=$$$$[t=\sqrt{x+1}\to dx=2\sqrt{x+1}dt]$$$$=2\int t\sqrt{t^2+t-1}dt=$$$$=\int (2t+1)\sqrt{t^2+t-1}dt-\int \sqrt{t^2+t-1}dt=$$$$$$$$\int (2t+1)\sqrt{t^2+t-1}dt=$$$$[u=t^2+t-1\to dt=\frac{du}{2t+1}]$$$$=\int \sqrt{u}du=\frac{2}{3}\sqrt{u^3}=\frac{2}{3}\sqrt{{(t^2+t-1)}^3}=$$$$=\frac{2}{3}\sqrt{{(x+\sqrt{x+1})}^3}$$$$$$$$\int \sqrt{t^2+t-1}dt=\int \sqrt{{(t+\frac{1}{2})}^2-\frac{5}{4}}dt=$$$$=\frac{1}{2}\int \sqrt{{(2t+1)}^2-5}dt=$$$$[v=2t+1\to dt=\frac{dv}{2}]$$$$=\frac{1}{4}\int \sqrt{v^2-5}dv=$$$$=\frac{1}{4}\left(\frac{1}{2}(v\sqrt{v^2-5}-5\ln (v+\sqrt{v^2-5}))\right)=$$$$=\frac{1}{8}(2t+1)\sqrt{{(2t+1)}^2-5}-$$$$-\frac{5}{8}\ln (2t+1+\sqrt{{(2t+1)}^2-5})=$$$$=\frac{1}{4}(1+2\sqrt{x+1})\sqrt{x+\sqrt{x+1}}-$$$$-\frac{5}{8}\ln (1+2\sqrt{x+1}+2\sqrt{x+\sqrt{x+1}})$$$$$$$$=\frac{1}{12}\sqrt{x+\sqrt{x+1}}(8x-3+2\sqrt{x+1})+\frac{5}{8}\ln (1+2\sqrt{x+1}+2\sqrt{x+\sqrt{x+1}})+C$$

Commented by prof Abdo imad last updated on 19/Jun/18

$$thankssirMjsyouarereallytalented.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com