
Question and Answers Forum
Question Number 40147 by maxmathsup by imad last updated on 16/Jul/18
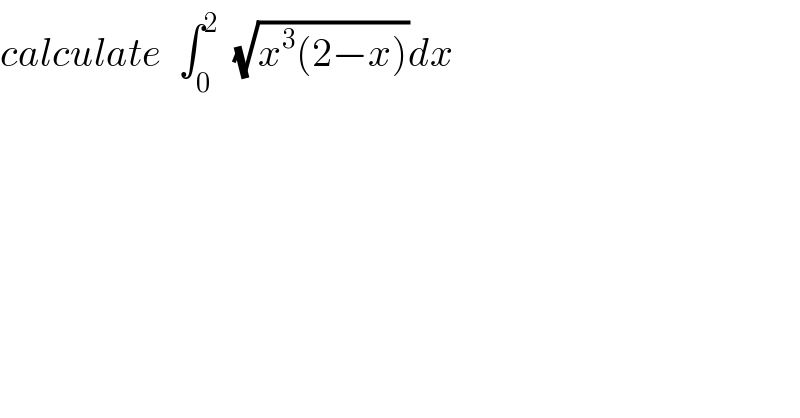
Commented by math khazana by abdo last updated on 17/Jul/18
![let I = ∫_0 ^2 (√(x^3 (2−x)))dx I =∫_0 ^2 x(√(x(2−x))) changement x=2sin^2 θ give I = ∫_0 ^(π/2) 2 sin^2 θ(√(2sin^2 θ(2−2sin^2 θ))) 4 sinθ cosθdθ =16∫_0 ^(π/2) sin^2 θ sinθ cosθ sinθ cosθ dθ =16 ∫_0 ^(π/2) sin^4 θ cos^2 θdθdθ by parts ∫_0 ^(π/2) cosθ( cosθ sin^4 θ)dθ =[(1/5) sin^5 θ cosθ]_0 ^(π/2) +∫_0 ^(π/2) (1/5) sin^5 θ sinθ dθ =(1/5) ∫_0 ^(π/2) (sin^2 θ)^3 dθ =(1/5) ∫_0 ^(π/2) {((1−cos(2θ))/2)}^3 dθ =(1/(40)) ∫_0 ^(π/2) {Σ_(k=0) ^3 C_3 ^k (−1)^k (cos(2θ))^k }dθ =(1/(40)) ∫_0 ^(π/2) {1 −3cos(2θ) +3cos^2 (2θ) −cos^3 (2θ)}dθ =(π/(80)) −(3/(40)) ∫_0 ^(π/2) cos(2θ)dθ +(3/(40)) ∫_0 ^(π/2) ((1+cos(4θ))/2)dθ −(1/(40)) ∫_0 ^(π/2) cos(2θ)((1+cos(4θ))/2) dθ =(π/(80)) +(3/(160)) −(1/(80)) ∫_0 ^(π/2) (1+cos(4θ))cos(2θ) ....be continued...](Q40205.png)
Commented by math khazana by abdo last updated on 25/Jul/18

| ||
Question and Answers Forum | ||
Question Number 40147 by maxmathsup by imad last updated on 16/Jul/18 | ||
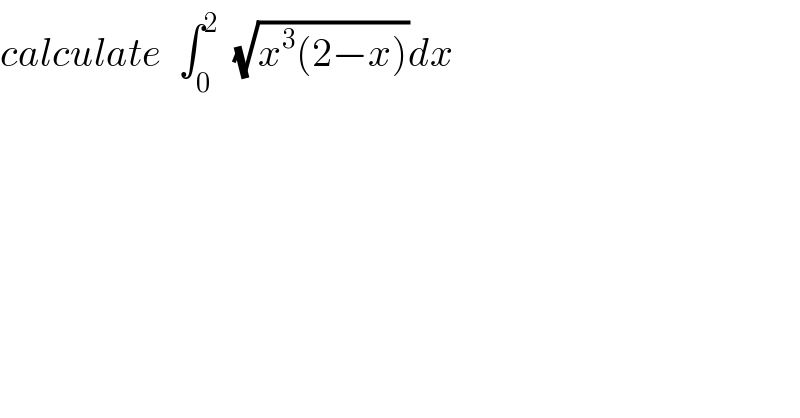 | ||
Commented by math khazana by abdo last updated on 17/Jul/18 | ||
![let I = ∫_0 ^2 (√(x^3 (2−x)))dx I =∫_0 ^2 x(√(x(2−x))) changement x=2sin^2 θ give I = ∫_0 ^(π/2) 2 sin^2 θ(√(2sin^2 θ(2−2sin^2 θ))) 4 sinθ cosθdθ =16∫_0 ^(π/2) sin^2 θ sinθ cosθ sinθ cosθ dθ =16 ∫_0 ^(π/2) sin^4 θ cos^2 θdθdθ by parts ∫_0 ^(π/2) cosθ( cosθ sin^4 θ)dθ =[(1/5) sin^5 θ cosθ]_0 ^(π/2) +∫_0 ^(π/2) (1/5) sin^5 θ sinθ dθ =(1/5) ∫_0 ^(π/2) (sin^2 θ)^3 dθ =(1/5) ∫_0 ^(π/2) {((1−cos(2θ))/2)}^3 dθ =(1/(40)) ∫_0 ^(π/2) {Σ_(k=0) ^3 C_3 ^k (−1)^k (cos(2θ))^k }dθ =(1/(40)) ∫_0 ^(π/2) {1 −3cos(2θ) +3cos^2 (2θ) −cos^3 (2θ)}dθ =(π/(80)) −(3/(40)) ∫_0 ^(π/2) cos(2θ)dθ +(3/(40)) ∫_0 ^(π/2) ((1+cos(4θ))/2)dθ −(1/(40)) ∫_0 ^(π/2) cos(2θ)((1+cos(4θ))/2) dθ =(π/(80)) +(3/(160)) −(1/(80)) ∫_0 ^(π/2) (1+cos(4θ))cos(2θ) ....be continued...](Q40205.png) | ||
Commented by math khazana by abdo last updated on 25/Jul/18 | ||
 | ||