
Question and Answers Forum
Question Number 93265 by abdomathmax last updated on 12/May/20

Commented by mathmax by abdo last updated on 12/May/20
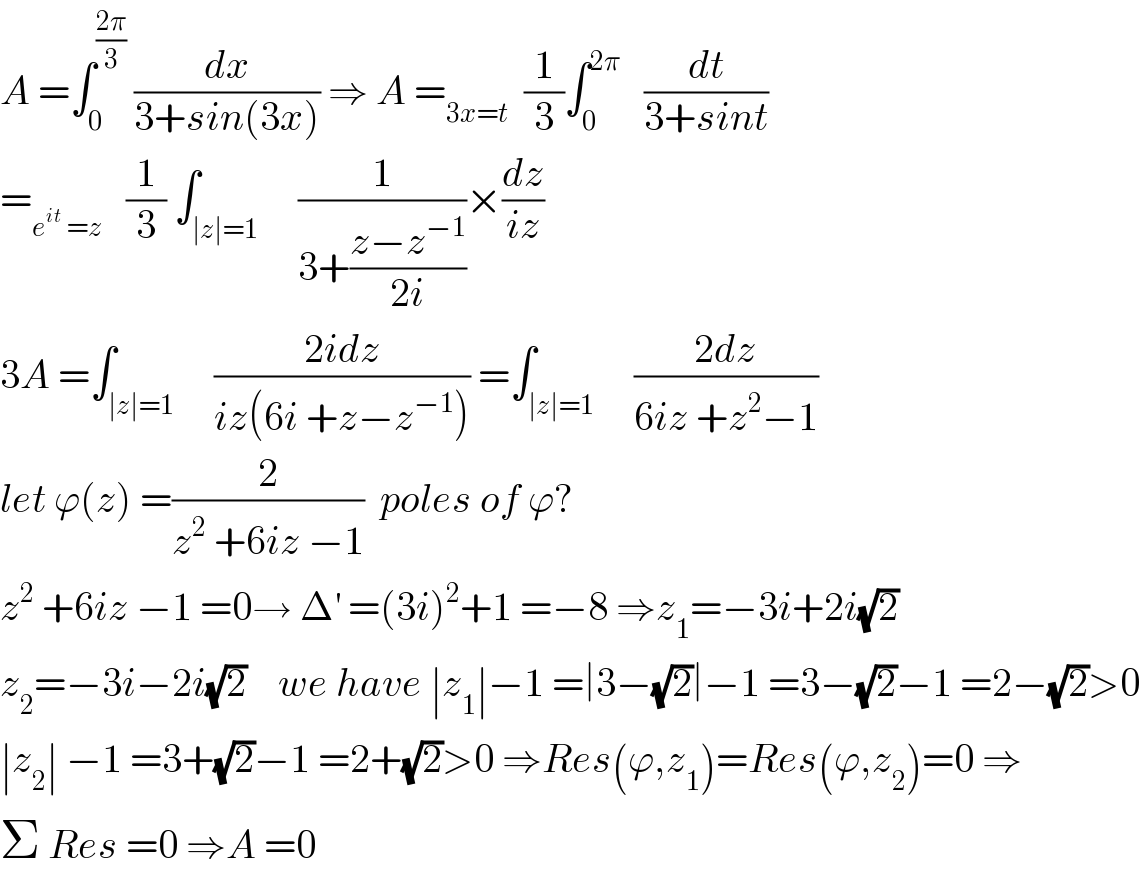
Answered by niroj last updated on 12/May/20
![∫_0 ^( ((2π)/3)) (( dx)/(3 + sin (3x))) Put , 3x= t 3dx=dt dx=(1/3)dt IF x=((2π)/3) ⇒ t= 2π IF x=0 ⇒ t=0 (1/3)∫_0 ^( 2π) (( 1)/(3+sin t))dt =[ (1/3)∫ (( 1)/(3+ ((2tan(t/2))/(1+tan^2 (t/2)))))dt]_0 2π = [ (1/3)∫(( sec^2 (t/2))/(3+3tan^2 (t/2)+2tan(t/2)))dt]_0 ^(2π) Put, tan (t/2)= m sec^2 (t/2)dt=2dm [ (1/3)∫ ((2dm)/(3+3m^2 +2m))]_0 ^(2π) = [(2/3)∫ (1/(3(m^2 +(2/3)m+1)))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m)^2 +2.(1/3).m+(1/9)−(1/9)+1))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m+(1/3))^2 −((8/9))))dm]_0 ^(2π) = [ (2/9)∫ (1/((m+(1/3))^2 −(((√8)/3))^2 ))dm]_0 ^(2π) = [(2/9).(1/(2.((√8)/3)))log (( m+(1/3) +((√8)/3))/(m+(1/3) −((√8)/3)))]_0 ^(2π) =[ (1/(3(√8))) log ((3m+1+(√8))/(3m+1−(√8)))]_0 ^(2π) = [(1/(3(√8)))log ((3 tan(t/2) +1+(√8))/(3tan(t/2) +1−(√8)))]_0 ^(2π) = {(1/(3(√8)))log ((3tan ((2π)/2)+1+(√8))/(3tan((2π)/2)+1−(√8)))}−{(1/(3(√8)))log ((3.0+1+(√8))/(3.0+1−(√8)))} = (1/(3(√8))) log ((1+(√8))/(1−(√8))) −(1/(3(√8)))log ((1+(√8))/(1−(√8))) = 0 //.](Q93273.png)
| ||
Question and Answers Forum | ||
Question Number 93265 by abdomathmax last updated on 12/May/20 | ||
 | ||
Commented by mathmax by abdo last updated on 12/May/20 | ||
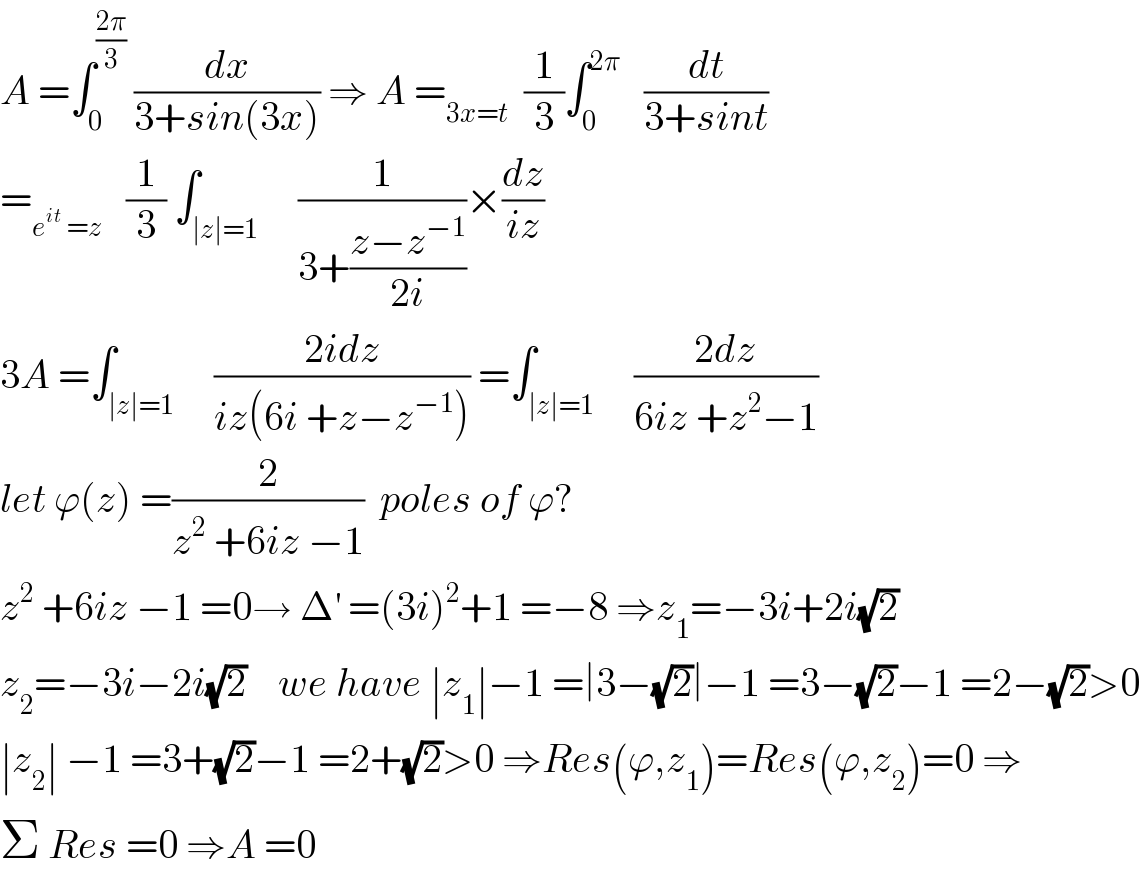 | ||
Answered by niroj last updated on 12/May/20 | ||
![∫_0 ^( ((2π)/3)) (( dx)/(3 + sin (3x))) Put , 3x= t 3dx=dt dx=(1/3)dt IF x=((2π)/3) ⇒ t= 2π IF x=0 ⇒ t=0 (1/3)∫_0 ^( 2π) (( 1)/(3+sin t))dt =[ (1/3)∫ (( 1)/(3+ ((2tan(t/2))/(1+tan^2 (t/2)))))dt]_0 2π = [ (1/3)∫(( sec^2 (t/2))/(3+3tan^2 (t/2)+2tan(t/2)))dt]_0 ^(2π) Put, tan (t/2)= m sec^2 (t/2)dt=2dm [ (1/3)∫ ((2dm)/(3+3m^2 +2m))]_0 ^(2π) = [(2/3)∫ (1/(3(m^2 +(2/3)m+1)))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m)^2 +2.(1/3).m+(1/9)−(1/9)+1))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m+(1/3))^2 −((8/9))))dm]_0 ^(2π) = [ (2/9)∫ (1/((m+(1/3))^2 −(((√8)/3))^2 ))dm]_0 ^(2π) = [(2/9).(1/(2.((√8)/3)))log (( m+(1/3) +((√8)/3))/(m+(1/3) −((√8)/3)))]_0 ^(2π) =[ (1/(3(√8))) log ((3m+1+(√8))/(3m+1−(√8)))]_0 ^(2π) = [(1/(3(√8)))log ((3 tan(t/2) +1+(√8))/(3tan(t/2) +1−(√8)))]_0 ^(2π) = {(1/(3(√8)))log ((3tan ((2π)/2)+1+(√8))/(3tan((2π)/2)+1−(√8)))}−{(1/(3(√8)))log ((3.0+1+(√8))/(3.0+1−(√8)))} = (1/(3(√8))) log ((1+(√8))/(1−(√8))) −(1/(3(√8)))log ((1+(√8))/(1−(√8))) = 0 //.](Q93273.png) | ||
| ||