
Question and Answers Forum
Question Number 89714 by abdomathmax last updated on 18/Apr/20
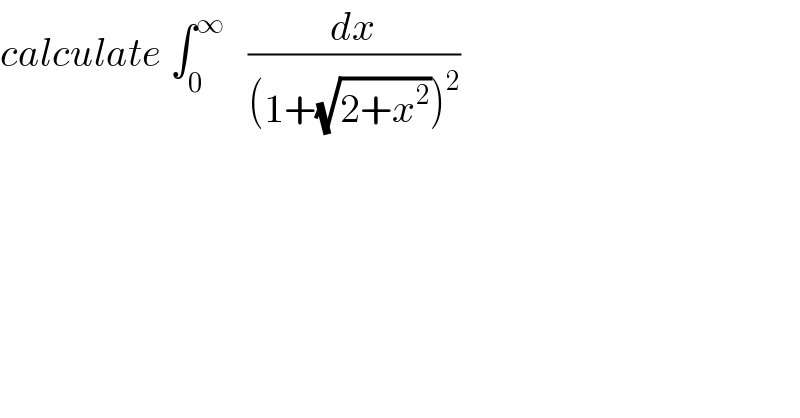
Commented by mathmax by abdo last updated on 19/Apr/20
![parametric method let f(t)=∫_0 ^∞ (dx/(t+(√(2+x^2 )))) with t>0 f^′ (t)=−∫_0 ^∞ (dx/((t+(√(2+x^2 )))^2 )) ⇒∫_0 ^∞ (dx/((t+(√(2+x^2 )))^2 )) =−f^′ (t) changement x =(√2)sh(u) give f(t)=∫_0 ^∞ (((√2)ch(u)du)/(t +(√2)ch(u))) =(√2)∫_0 ^∞ (((e^u +e^(−u) )/2)/(t+(√2)×((e^u +e^(−u) )/2)))du =(√2)∫_0 ^∞ ((e^u +e^(−u) )/(2t+(√2)e^u +(√2)e^(−u) ))du =_(e^u =z) (√2)∫_1 ^∞ ((z+z^(−1) )/(2t+(√2)z +(√2)z^(−1) ))×(dz/z) =(√2)∫_1 ^(+∞) ((z+z^(−1) )/(2tz +(√2)z^2 +(√2))) dz =(√2)∫_1 ^(+∞) ((z^2 +1)/(z((√2)z^2 +2tz +(√2))))dz decoposition of g(z)=((z^2 +1)/(z((√2)z^2 +2tz +(√2)))) (√2)z^2 +2tz +(√2)=0 →Δ^′ =t^2 −2<0 if t<(√2) z_1 =((−t+i(√(2−t^2 )))/(√2)) and z_2 =((−t−i(√(2−t^2 )))/(√2)) g(z)=((z^2 +1)/((√2)z(z−z_1 )(z−z_2 ))) =(a/z) +(b/(z−z_1 )) +(c/(z−z_2 )) a =(1/((√2)z_1 z_2 )) =(1/(√2)) ,b =((z_1 ^2 +1)/((√2)z_1 (√2)i(√(2−t^2 )))) =((1+z_1 ^2 )/(2iz_1 (√(2−t^2 )))) b=((z_2 ^2 +1)/((√2)z_2 (−(√2)i(√(2−t^2 ))))) =((1+z_2 ^2 )/(−2iz_2 (√(2−t^2 )))) ⇒ ∫_1 ^(+∞) g(z)dz =∫_1 ^(+∞) ((a/z)+(b/(z−z_1 )) +(c/(z−z_2 )))dz =[aln∣z∣ +bln∣z−z_1 ∣ +cln∣z−z_2 ∣]_1 ^(+∞) rest to simplify b and c be continued...](Q89825.png)
Answered by MJS last updated on 18/Apr/20
![∫(dx/((1+(√(x^2 +2)))^2 ))= [t=((x+(√(x^2 +2)))/(√2)) → dx=((√(2(x^2 +2)))/(x+(√(x^2 +2))))dt] =(√2)∫((t^2 +1)/((t^2 +(√2)t+1)^2 ))dt= [Ostrogradski] =(((√2)t+2)/(t^2 +(√2)t+1))+2(√2)∫(dt/(t^2 +(√2)t+1))= =(((√2)t+2)/(t^2 +(√2)t+1))+4arctan ((√2)t+1) = =((x^2 +x+1−x(√(x^2 +2)))/(x^2 +1))+4arctan (x+1+(√(x^2 +2))) +C ⇒ ∫_0 ^∞ (dx/((1+(√(x^2 +2)))^2 ))=(π/2)−1](Q89721.png)
Commented by turbo msup by abdo last updated on 18/Apr/20

| ||
Question and Answers Forum | ||
Question Number 89714 by abdomathmax last updated on 18/Apr/20 | ||
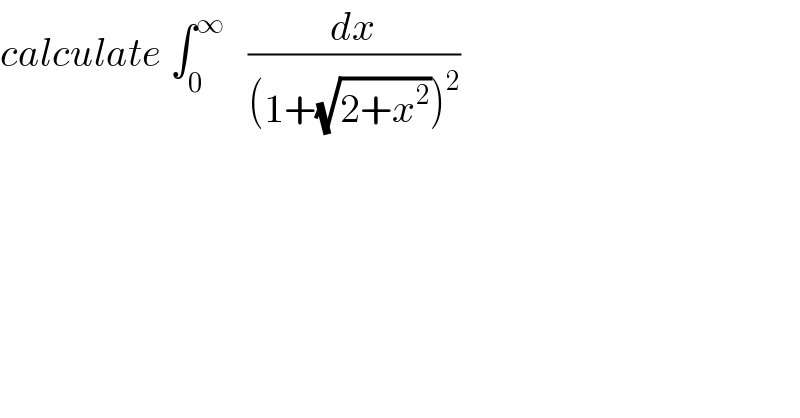 | ||
Commented by mathmax by abdo last updated on 19/Apr/20 | ||
![parametric method let f(t)=∫_0 ^∞ (dx/(t+(√(2+x^2 )))) with t>0 f^′ (t)=−∫_0 ^∞ (dx/((t+(√(2+x^2 )))^2 )) ⇒∫_0 ^∞ (dx/((t+(√(2+x^2 )))^2 )) =−f^′ (t) changement x =(√2)sh(u) give f(t)=∫_0 ^∞ (((√2)ch(u)du)/(t +(√2)ch(u))) =(√2)∫_0 ^∞ (((e^u +e^(−u) )/2)/(t+(√2)×((e^u +e^(−u) )/2)))du =(√2)∫_0 ^∞ ((e^u +e^(−u) )/(2t+(√2)e^u +(√2)e^(−u) ))du =_(e^u =z) (√2)∫_1 ^∞ ((z+z^(−1) )/(2t+(√2)z +(√2)z^(−1) ))×(dz/z) =(√2)∫_1 ^(+∞) ((z+z^(−1) )/(2tz +(√2)z^2 +(√2))) dz =(√2)∫_1 ^(+∞) ((z^2 +1)/(z((√2)z^2 +2tz +(√2))))dz decoposition of g(z)=((z^2 +1)/(z((√2)z^2 +2tz +(√2)))) (√2)z^2 +2tz +(√2)=0 →Δ^′ =t^2 −2<0 if t<(√2) z_1 =((−t+i(√(2−t^2 )))/(√2)) and z_2 =((−t−i(√(2−t^2 )))/(√2)) g(z)=((z^2 +1)/((√2)z(z−z_1 )(z−z_2 ))) =(a/z) +(b/(z−z_1 )) +(c/(z−z_2 )) a =(1/((√2)z_1 z_2 )) =(1/(√2)) ,b =((z_1 ^2 +1)/((√2)z_1 (√2)i(√(2−t^2 )))) =((1+z_1 ^2 )/(2iz_1 (√(2−t^2 )))) b=((z_2 ^2 +1)/((√2)z_2 (−(√2)i(√(2−t^2 ))))) =((1+z_2 ^2 )/(−2iz_2 (√(2−t^2 )))) ⇒ ∫_1 ^(+∞) g(z)dz =∫_1 ^(+∞) ((a/z)+(b/(z−z_1 )) +(c/(z−z_2 )))dz =[aln∣z∣ +bln∣z−z_1 ∣ +cln∣z−z_2 ∣]_1 ^(+∞) rest to simplify b and c be continued...](Q89825.png) | ||
Answered by MJS last updated on 18/Apr/20 | ||
![∫(dx/((1+(√(x^2 +2)))^2 ))= [t=((x+(√(x^2 +2)))/(√2)) → dx=((√(2(x^2 +2)))/(x+(√(x^2 +2))))dt] =(√2)∫((t^2 +1)/((t^2 +(√2)t+1)^2 ))dt= [Ostrogradski] =(((√2)t+2)/(t^2 +(√2)t+1))+2(√2)∫(dt/(t^2 +(√2)t+1))= =(((√2)t+2)/(t^2 +(√2)t+1))+4arctan ((√2)t+1) = =((x^2 +x+1−x(√(x^2 +2)))/(x^2 +1))+4arctan (x+1+(√(x^2 +2))) +C ⇒ ∫_0 ^∞ (dx/((1+(√(x^2 +2)))^2 ))=(π/2)−1](Q89721.png) | ||
| ||
Commented by turbo msup by abdo last updated on 18/Apr/20 | ||
 | ||