Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 51324 by Abdo msup. last updated on 25/Dec/18

$$calculate{\int }_0^{+\mathrm{\infty }}\frac{dx}{1+x^2+x^4}$$

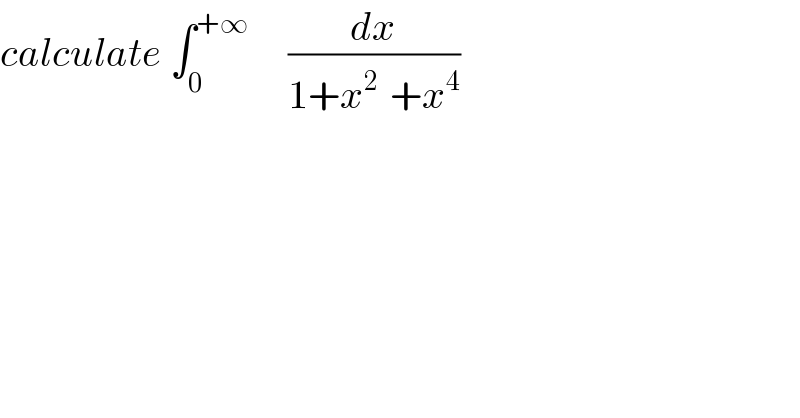
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18

$$\int \frac{dx}{x^4+x^2+1}$$$$\frac{1}{2}\int \frac{\frac{2}{x^2}}{x^2+1+\frac{1}{x^2}}$$$$\frac{1}{2}\int \frac{(1+\frac{1}{x^2})-(1-\frac{1}{x^2})}{(x^2+\frac{1}{x^2}+1)}dx$$$$\frac{1}{2}\int \frac{d(x-\frac{1}{x})}{{(x-\frac{1}{x})}^2+3}-\frac{1}{2}\int \frac{d(x+\frac{1}{x})}{{(x+\frac{1}{x})}^2-1}$$$$\frac{1}{2}\times \frac{1}{\sqrt{3}}{tan}^{-1}\left(\frac{x-\frac{1}{x}}{\sqrt{3}}\right)-\frac{1}{2}\times \frac{1}{2}ln\left(\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}\right)+c_1$$$$=\frac{1}{2\sqrt{3}}\times {tan}^{-1}\left(\frac{x^2-1}{x\sqrt{3}}\right)-\frac{1}{4}ln\left(\frac{x^2-x+1}{x^2+x+1}\right)+c_1$$$$requiredanswer$$$$=\mid \frac{1}{2\sqrt{3}}{tan}^{-1}\left(\frac{x^2-1}{x\sqrt{3}}\right)-\frac{1}{4}ln\left(\frac{1-\frac{1}{x}+\frac{1}{x^2}}{1+\frac{1}{x}+\frac{1}{x^2}}\right){\mid }_0^{\mathrm{\infty }}$$$$=\mid \frac{1}{2\sqrt{3}}{tan}^{-1}\left(\frac{1-\frac{1}{x^2}}{\frac{\sqrt{3}}{x}}\right)-do{\mid }_0^{\mathrm{\infty }}$$$$=\frac{1}{2\sqrt{3}}[{tan}^{-1}\left(\frac{1-0}{0}\right)-{tan}^{-1}\left(\frac{0^2-1}{0\times \sqrt{3}}\right)]-\frac{1}{4}[ln\left(\frac{1-0+0}{1+0+0}\right)-ln\left(\frac{0^2-0+1}{0^2+0+1}\right)]$$$$=\frac{1}{2\sqrt{3}}[tan\left(\mathrm{\infty }\right)-{tan}^{-1}(-\mathrm{\infty })]-do$$$$=\frac{1}{2\sqrt{3}}[\frac{\pi }{2}-\left(\frac{-\pi }{2}\right)]$$$$=\frac{\pi }{2\sqrt{3}}$$$$$$

Commented by peter frank last updated on 26/Dec/18

$$niceworksir$$

Answered by Smail last updated on 26/Dec/18

$$\frac{1}{(x^2+x+1)(x^2-x+1)}=\frac{ax+b}{x^2+x+1}+\frac{cx+d}{x^2-x+1}$$$$a=-c,d=1-b$$$$b=1-a$$$$a=b=-c=d=\frac{1}{2}$$$$A={\int }_0^{\mathrm{\infty }}\frac{dx}{1+x^2+x^4}=\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{x+1}{x^2+x+1}dx-\frac{1}{2}{\int }_0^{\mathrm{\infty }}\frac{x-1}{x^2-x+1}dx$$$$=\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{2x+1+1}{x^2+x+1}dx-\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{2x-1-1}{x^2-x+1}dx$$$$=\frac{1}{4}{[ln\mid \frac{x^2+x+1}{x^2-x+1}\mid ]}_0^{\mathrm{\infty }}+\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{dx}{{(x+\frac{1}{2})}^2+\frac{3}{4}}+\frac{1}{4}{\int }_0^{\mathrm{\infty }}\frac{dx}{{(x-\frac{1}{2})}^2+\frac{3}{4}}$$$$=\frac{1}{3}{\int }_0^{\mathrm{\infty }}\frac{dx}{{\left(\frac{2x+1}{\sqrt{3}}\right)}^2+1}+\frac{1}{3}{\int }_0^{\mathrm{\infty }}\frac{dx}{{\left(\frac{2x-1}{\sqrt{3}}\right)}^2+1}$$$$t=\frac{2x\underset{-}{+}1}{\sqrt{3}}\Rightarrow dx=\frac{\sqrt{3}}{2}dt$$$$A=\frac{1}{2\sqrt{3}}{\int }_{1/\sqrt{3}}^{\mathrm{\infty }}\frac{dt}{t^2+1}+\frac{1}{2\sqrt{3}}{\int }_{-1/\sqrt{3}}^{\mathrm{\infty }}\frac{dt}{t^2+1}$$$$=\frac{1}{2\sqrt{3}}{\left[{tan}^{-1}\left(t\right)\right]}_{1/\sqrt{3}}^{\mathrm{\infty }}+\frac{1}{2\sqrt{3}}{\left[{tan}^{-1}\left(t\right)\right]}_{-1/\sqrt{3}}^{\mathrm{\infty }}$$$$=\frac{1}{2\sqrt{3}}(\frac{\pi }{2}-{tan}^{-1}\left(\frac{\sqrt{3}}{3}\right))+\frac{1}{2\sqrt{3}}(\frac{\pi }{2}+{tan}^{-1}\left(\frac{\sqrt{3}}{3}\right))$$$$=\frac{\pi }{2\sqrt{3}}$$

Commented by peter frank last updated on 26/Dec/18

$$niceworksir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com