
Question and Answers Forum
Question Number 27804 by abdo imad last updated on 15/Jan/18
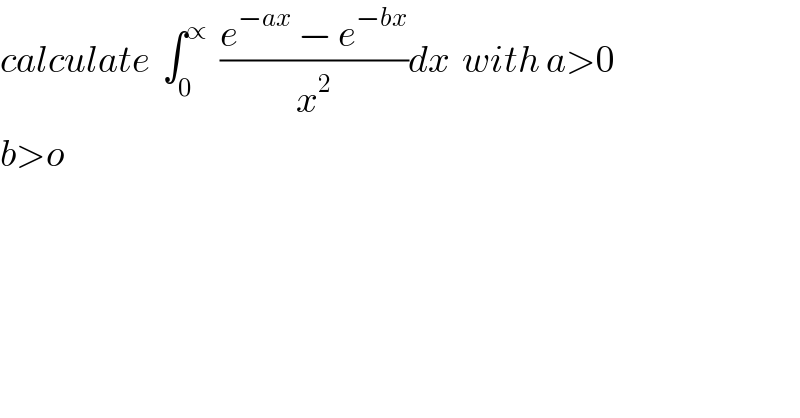
Commented by abdo imad last updated on 17/Jan/18
![let put I= ∫_0 ^∞ ((e^(−ax) −e^(−bx) )/x^2 )dx we have lim_(x→0 ) ((e^(−ax) −e^(−bx) )/x^2 ) =lim_(x→0 ) ((−a e^(−ax) +b e^(−bx) )/(2x)) =lim_(x→o) ((a^2 e^(−ax) −b^2 e^(−bx) )/2)= ((a^2 −b^2 )/2) for another side lim_(x→+∝) x^2 ((e^(−ax) −e^(−bx) )/x^2 ) =0 so the integral converges let integrate by parts u^′ =(1/x^2 ) and v= e^(−ax) −e^(−bx) I=[ −(1/x)( e^(−ax) − e^(−bx) )]_0 ^(+∝) − ∫_0 ^∞ −(1/x) ( −a e^(−ax) +b e^(−bx) )dx = b−a + ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x)dx let introduce f(t) = ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x) e^(−tx) dx with t≥0 f^′ (t)= −∫_0 ^∞ ( b e^(−bx) −a e^(−ax) ) e^(−tx) = a∫_0 ^∞ e^(−( t+a)x) dx −b∫_0 ^∞ e^(−(t+b)x) dx but ∫_0 ^∞ e^(−(t+a)x) dx=[ ((−1)/(t+a)) e^(−(t+a)x) ]_0 ^(+∝) = (1/(t+a)) and by same manner ∫_0 ^∞ e^(−(t+b)x) dx= (1/(t+b)) f^′ (t)= (a/(t+a)) − (b/(t+b)) ⇒ f(t)= aln/t+a/ −b ln/t+b/ +λ λ= lim_(t→+∝) (f(t) −aln/t+a/−bln/t+b/)=0 so f(t) = aln/t+a/ −bln/t+b/ but t≥0 and a>0 and b>0 f(t)= aln(t+a) −bln(t+b) and ∫_0 ^∞ ((b e^(−bx) − a e^(−ax) )/x)dx=f(0)= aln(a)−b lnb finally I = b−a +aln(a) −b ln(b) .](Q27963.png)
| ||
Question and Answers Forum | ||
Question Number 27804 by abdo imad last updated on 15/Jan/18 | ||
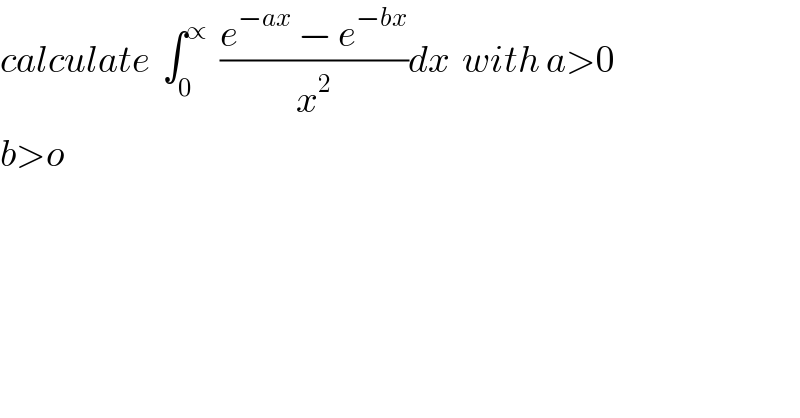 | ||
Commented by abdo imad last updated on 17/Jan/18 | ||
![let put I= ∫_0 ^∞ ((e^(−ax) −e^(−bx) )/x^2 )dx we have lim_(x→0 ) ((e^(−ax) −e^(−bx) )/x^2 ) =lim_(x→0 ) ((−a e^(−ax) +b e^(−bx) )/(2x)) =lim_(x→o) ((a^2 e^(−ax) −b^2 e^(−bx) )/2)= ((a^2 −b^2 )/2) for another side lim_(x→+∝) x^2 ((e^(−ax) −e^(−bx) )/x^2 ) =0 so the integral converges let integrate by parts u^′ =(1/x^2 ) and v= e^(−ax) −e^(−bx) I=[ −(1/x)( e^(−ax) − e^(−bx) )]_0 ^(+∝) − ∫_0 ^∞ −(1/x) ( −a e^(−ax) +b e^(−bx) )dx = b−a + ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x)dx let introduce f(t) = ∫_0 ^∞ ((b e^(−bx) −a e^(−ax) )/x) e^(−tx) dx with t≥0 f^′ (t)= −∫_0 ^∞ ( b e^(−bx) −a e^(−ax) ) e^(−tx) = a∫_0 ^∞ e^(−( t+a)x) dx −b∫_0 ^∞ e^(−(t+b)x) dx but ∫_0 ^∞ e^(−(t+a)x) dx=[ ((−1)/(t+a)) e^(−(t+a)x) ]_0 ^(+∝) = (1/(t+a)) and by same manner ∫_0 ^∞ e^(−(t+b)x) dx= (1/(t+b)) f^′ (t)= (a/(t+a)) − (b/(t+b)) ⇒ f(t)= aln/t+a/ −b ln/t+b/ +λ λ= lim_(t→+∝) (f(t) −aln/t+a/−bln/t+b/)=0 so f(t) = aln/t+a/ −bln/t+b/ but t≥0 and a>0 and b>0 f(t)= aln(t+a) −bln(t+b) and ∫_0 ^∞ ((b e^(−bx) − a e^(−ax) )/x)dx=f(0)= aln(a)−b lnb finally I = b−a +aln(a) −b ln(b) .](Q27963.png) | ||