
Question and Answers Forum
Question Number 31077 by abdo imad last updated on 02/Mar/18
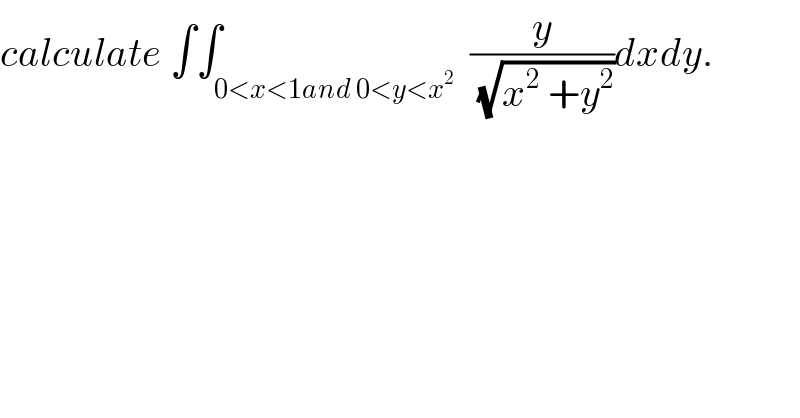
Commented by abdo imad last updated on 07/Mar/18
![I= ∫_0 ^1 ( ∫_0 ^x^2 (y/(√(x^2 +y^2 )))dy)dx but ∫_0 ^x^2 (y/(√(x^2 +y^2 )))dy= [(√(x^2 +y^2 ))^ ]_(y=0) ^(y=x^2 ) =(√(x^2 +x^4 )) −x ⇒ I= ∫_0 ^1 ((√(x^2 +x^4 )) −x)dx =∫_0 ^1 (√(x^2 +x^4 )) dx −(1/2) but ∫_0 ^1 (√(x^2 +x^4 )) dx=∫_0 ^1 x(√(1+x^2 )) dx =(1/2) ∫_0 ^1 (2x)(1+x^2 )^(1/2) dx =(1/2) [ (2/3)(1+x^2 )^(3/2) ]_0 ^1 =(1/3)( 2^(3/2) −1)=(1/3)(2(√2) −1) ⇒ I=((2(√2))/3) −(1/3) −(1/2)=((2(√2))/3) −(5/6) .](Q31396.png)
| ||
Question and Answers Forum | ||
Question Number 31077 by abdo imad last updated on 02/Mar/18 | ||
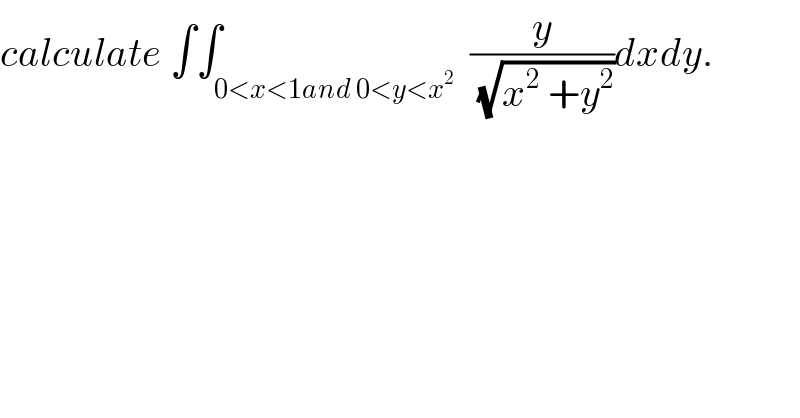 | ||
Commented by abdo imad last updated on 07/Mar/18 | ||
![I= ∫_0 ^1 ( ∫_0 ^x^2 (y/(√(x^2 +y^2 )))dy)dx but ∫_0 ^x^2 (y/(√(x^2 +y^2 )))dy= [(√(x^2 +y^2 ))^ ]_(y=0) ^(y=x^2 ) =(√(x^2 +x^4 )) −x ⇒ I= ∫_0 ^1 ((√(x^2 +x^4 )) −x)dx =∫_0 ^1 (√(x^2 +x^4 )) dx −(1/2) but ∫_0 ^1 (√(x^2 +x^4 )) dx=∫_0 ^1 x(√(1+x^2 )) dx =(1/2) ∫_0 ^1 (2x)(1+x^2 )^(1/2) dx =(1/2) [ (2/3)(1+x^2 )^(3/2) ]_0 ^1 =(1/3)( 2^(3/2) −1)=(1/3)(2(√2) −1) ⇒ I=((2(√2))/3) −(1/3) −(1/2)=((2(√2))/3) −(5/6) .](Q31396.png) | ||