calculate ∫_0 ^(π/2) ((cos^2 x)/(cosx +sinx))dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 65691 by mathmax by abdo last updated on 02/Aug/19

$c a l c u l a t e \int_{0}^{\frac{π}{2}} \frac{{c o s}^{2} x}{c o s x + s i n x} d x$
Commented by mathmax by abdo last updated on 02/Aug/19

$t a n (\frac{u}{2}) m e t h o d l e t I = \int_{0}^{\frac{π}{2}} \frac{{c o s}^{2} x}{c o s x + s i n x} d x \Rightarrow I = \int_{0}^{\frac{π}{2}} \frac{c o s x}{1 + t a n x} d x$ $c h a n g e m e n t t a n (\frac{x}{2}) = t g i v e I = \int_{0}^{1} \frac{\frac{1 - t^{2}}{1 + t^{2}}}{1 + \frac{2 t}{1 - t^{2}}} \frac{2 d t}{1 + t^{2}}$ $= 2 \int_{0}^{1} \frac{1 - t^{2}}{{(1 + t^{2})}^{2}} \frac{1 - t^{2}}{1 - t^{2} + 2 t} d t = 2 \int_{0}^{1} \frac{{(1 - t^{2})}^{2}}{(1 + t^{2}) (- t^{2} + 2 t + 1)} d t$ $= - 2 \int_{0}^{1} \frac{{(1 - t^{2})}^{2}}{(1 + t^{2}) (t^{2} - 2 t - 1)} d t l e t d e c o m p o s e$ $F (t) = \frac{t^{4} - 2 t^{2} + 1}{(t^{2} + 1) (t^{2} - 2 t - 1)} \Rightarrow F (t) = \frac{t^{4} - 2 t^{2} + 1}{t^{4} - 2 t^{3} - t^{2} + t^{2} - 2 t - 1}$ $= \frac{t^{4} - 2 t^{2} + 1}{t^{4} - 2 t^{3} - 2 t - 1} \Rightarrow F (t) - 1 = \frac{t^{4} - 2 t^{2} + 1 - t^{4} + 2 t^{3} + 2 t + 1}{t^{4} - 2 t^{3} - 2 t - 1}$ $= \frac{2 t^{3} - 2 t^{2} + 2 t + 2}{(t^{2} + 1) (t^{2} - 2 t - 1)} = G (t) = \frac{a t + b}{t^{2} + 1} + \frac{c}{t - t_{1}} + \frac{d}{t - t_{2}}$ $Δ^{^{'}} = 1 + 1 = 2 \Rightarrow t_{1} = 1 + \sqrt{2} a n d t_{2} = 1 - \sqrt{2}$ $c = {l i m}_{t \to t_{1}} (t - t_{1}) G (t) = \frac{2 t_{1}^{3} - 2 t_{1}^{2} + 2 t_{1} + 2}{(t_{1}^{2} + 1) (t_{1} - t_{2})} (t_{1} - t_{2} = 2 \sqrt{2})$ $d = {l i m}_{t \to t_{2}} (t - t_{2}) G (t_{2}) = \frac{2 t_{2}^{3} - 2 t_{2}^{2} + 2 t_{2} + 2}{(t_{2}^{2} + 1) (t_{2} - t_{1})}$ ${l i m}_{t \to + \infty} t G (t) = 2 = a + c + d \Rightarrow a = 2 - c - d$ $G (0) = - 2 = b - \frac{c}{t_{1}} - \frac{d}{t_{2}} \Rightarrow b = \frac{c}{t_{1}} + \frac{d}{t_{2}} - 2 r e s t t o s i m p l i f y t h e$ $c a l c u l u s \Rightarrow \int F (t) d t = t + \int G (t) d t$ $= t + c l n ∣ t - t_{1} ∣ + d ∣ t - t_{2} ∣ + \frac{a}{2} l n (t^{2} + 1) + b a r c t a n t + λ$ $. . . . b e c o n t i n u e d . . . .$
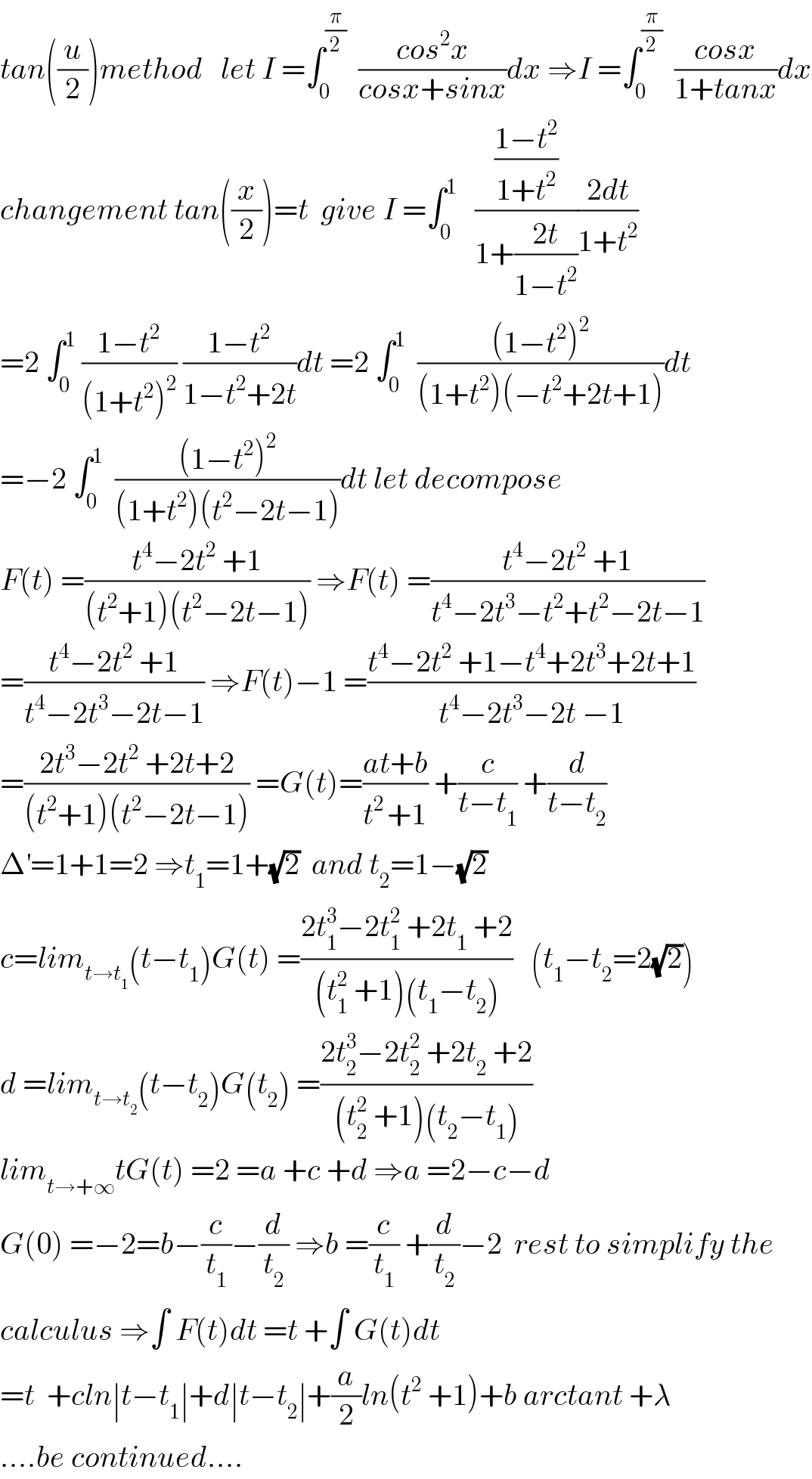
	Answered by Tanmay chaudhury last updated on 02/Aug/19

	$I = \int_{0}^{\frac{π}{2}} \frac{{c o s}^{2} x}{c o s x + s i n x} d x$ $I = \int_{0}^{\frac{π}{2}} \frac{{c o s}^{2} (\frac{π}{2} - x)}{c o s (\frac{π}{2} - x) + s i n (\frac{π}{2} - x)} d x$ $= \int_{0}^{\frac{π}{2}} \frac{{s i n}^{2} x}{s i n x + c o s x} d x$ $2 I = \int_{0}^{\frac{π}{2}} \frac{d x}{s i n x + c o s x}$ $2 I = \int_{0}^{\frac{π}{2}} \frac{d x}{\sqrt{2} (\frac{1}{\sqrt{2}} s i n x + \frac{1}{\sqrt{2}} c o s x)}$ $I = \frac{1}{2 \sqrt{2}} \int_{0}^{\frac{π}{2}} \frac{d x}{s i n (\frac{π}{4} + x)}$ $I = \frac{1}{2 \sqrt{2}} \int_{0}^{\frac{π}{4}} c o s e c (\frac{π}{4} + x) d x$ $I = \frac{1}{2 \sqrt{2}} ∣ l n t a n (\frac{\frac{π}{4} + x}{2}) ∣_{0}^{\frac{π}{4}}$ $= \frac{1}{2 \sqrt{2}} [l n t a n (\frac{π}{4}) - l n t a n (\frac{π}{8})]$ $= \frac{- 1}{2 \sqrt{2}} l n t a n (\frac{π}{8})$
	Commented by mathmax by abdo last updated on 02/Aug/19

	$t h a n k y o u s i r t a n m a y$
	Commented by Tanmay chaudhury last updated on 02/Aug/19

	$m o s t e e l c o m e s i r . . .$
	Commented by peter frank last updated on 02/Aug/19

	$t h a n k y o u$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum