
Question and Answers Forum
Question Number 50415 by Abdo msup. last updated on 16/Dec/18
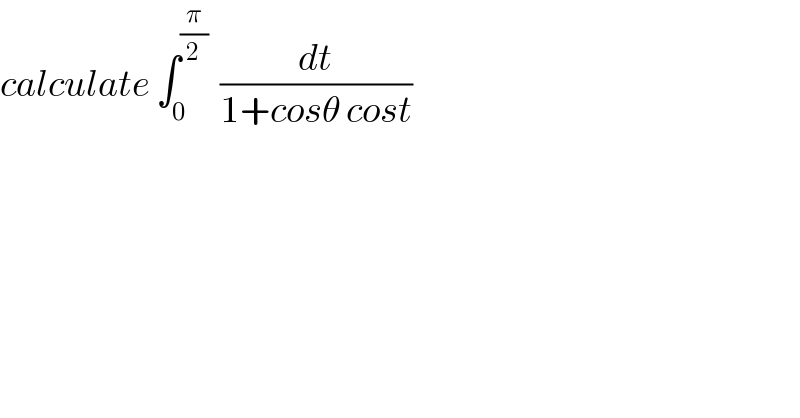
Commented by Abdo msup. last updated on 18/Dec/18
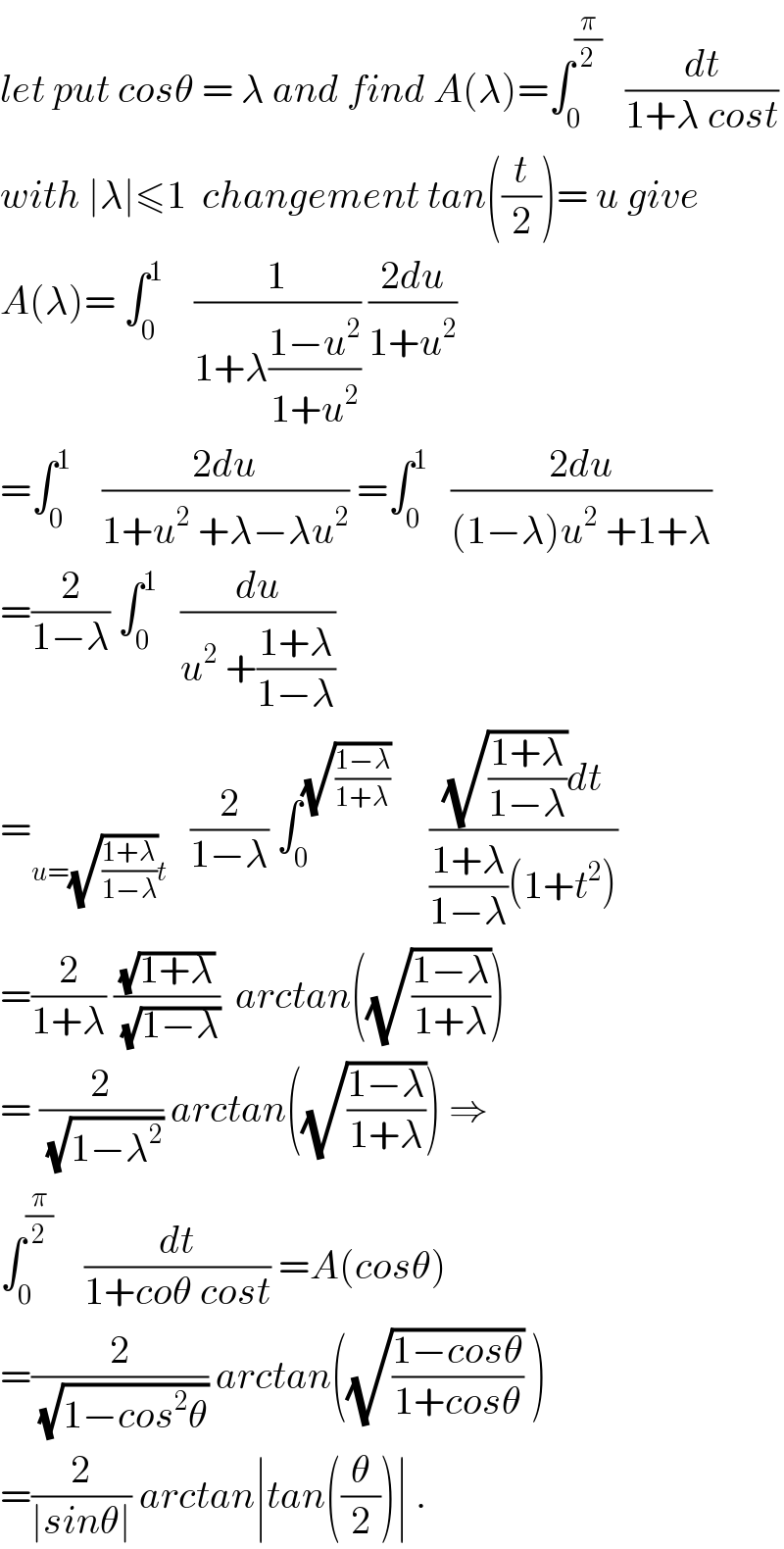
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
![∫(dt/(1+cosθcost)) (1/(cosθ))∫(dt/(secθ+cost)) (1/(cosθ))∫(dt/(secθ+((1−tan^2 (t/2))/(1+tan^2 (t/2))))) (1/(cosθ))∫((sec^2 (t/2)dt)/(secθ+secθtan^2 (t/2)+1−tan^2 (t/2))) =secθ∫((sec^2 (t/2)×dt)/((secθ+1)+tan^2 (t/2)(secθ−1))) =secθ∫((sec^2 (t/2))/((secθ−1){((secθ+1)/(secθ−1))+tan^2 (t/2)}))dt =((secθ)/(secθ−1))∫((sec^2 (t/2))/(((1+cosθ)/(1−cosθ))+tan^2 (t/2)))dt =(1/(1−cosθ))∫((sec^2 (t/2)dt)/(cot^2 (θ/2)+tan^2 (t/2))) k=tan(t/2) dk=(1/2)sec^2 (t/2)dt =(1/(2sin^2 (θ/2)))∫((2dk)/(cot^2 (θ/2)+k^2 )) =(1/(sin^2 (θ/2)))∫(dk/(cot^2 (θ/2)+k^2 )) =(1/(sin^2 (θ/2)))×(1/(cot(θ/2)))tan^(−1) ((k/(cot(θ/2)))) =(2/(sinθ))tan^(−1) (((tan(t/2))/(cot(θ/2))))+c required answer iz (2/(sinθ))∣tan^(−1) (((tan(t/2))/(cot(θ/2))))∣_0 ^(π/2) =(2/(sinθ))[tan^(−1) (((tan(π/4))/(cot(θ/2))))−tan^(−1) (((tan0)/(cot(θ/2))))] =(2/(sinθ))[tan^(−1) (tan(θ/2))] =(2/(sinθ))×(θ/2)=(θ/(sinθ))](Q50539.png)
| ||
Question and Answers Forum | ||
Question Number 50415 by Abdo msup. last updated on 16/Dec/18 | ||
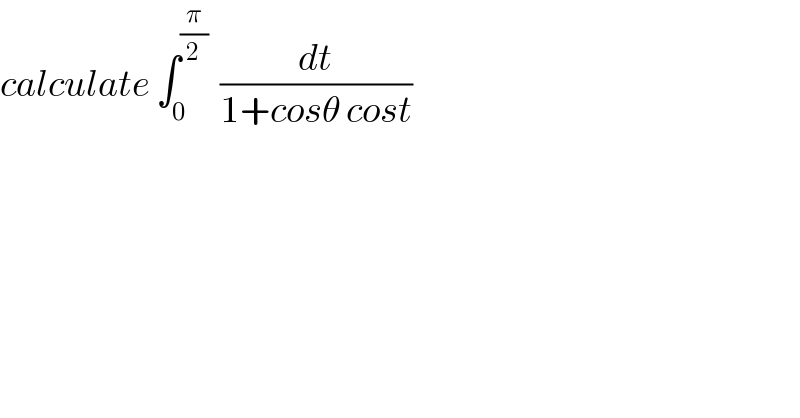 | ||
Commented by Abdo msup. last updated on 18/Dec/18 | ||
 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18 | ||
![∫(dt/(1+cosθcost)) (1/(cosθ))∫(dt/(secθ+cost)) (1/(cosθ))∫(dt/(secθ+((1−tan^2 (t/2))/(1+tan^2 (t/2))))) (1/(cosθ))∫((sec^2 (t/2)dt)/(secθ+secθtan^2 (t/2)+1−tan^2 (t/2))) =secθ∫((sec^2 (t/2)×dt)/((secθ+1)+tan^2 (t/2)(secθ−1))) =secθ∫((sec^2 (t/2))/((secθ−1){((secθ+1)/(secθ−1))+tan^2 (t/2)}))dt =((secθ)/(secθ−1))∫((sec^2 (t/2))/(((1+cosθ)/(1−cosθ))+tan^2 (t/2)))dt =(1/(1−cosθ))∫((sec^2 (t/2)dt)/(cot^2 (θ/2)+tan^2 (t/2))) k=tan(t/2) dk=(1/2)sec^2 (t/2)dt =(1/(2sin^2 (θ/2)))∫((2dk)/(cot^2 (θ/2)+k^2 )) =(1/(sin^2 (θ/2)))∫(dk/(cot^2 (θ/2)+k^2 )) =(1/(sin^2 (θ/2)))×(1/(cot(θ/2)))tan^(−1) ((k/(cot(θ/2)))) =(2/(sinθ))tan^(−1) (((tan(t/2))/(cot(θ/2))))+c required answer iz (2/(sinθ))∣tan^(−1) (((tan(t/2))/(cot(θ/2))))∣_0 ^(π/2) =(2/(sinθ))[tan^(−1) (((tan(π/4))/(cot(θ/2))))−tan^(−1) (((tan0)/(cot(θ/2))))] =(2/(sinθ))[tan^(−1) (tan(θ/2))] =(2/(sinθ))×(θ/2)=(θ/(sinθ))](Q50539.png) | ||
| ||