
Question and Answers Forum
Question Number 50414 by Abdo msup. last updated on 16/Dec/18
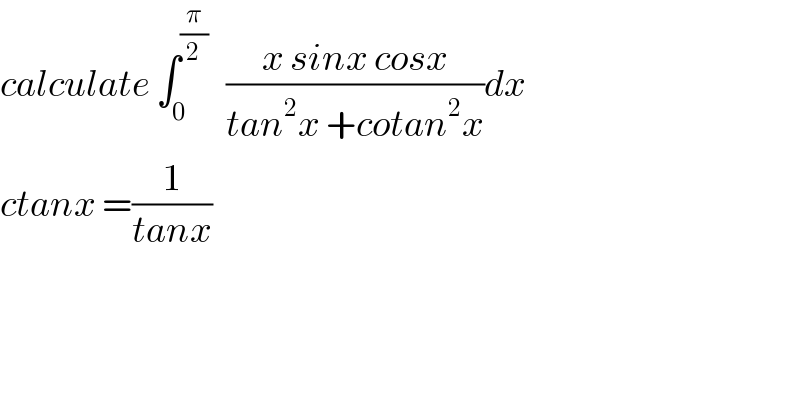
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18
![I=∫_0 ^(π/2) ((((π/2)−x)cosxsinx)/(cot^2 x+tan^2 x))dx 2I=∫_0 ^(π/2) ((((π/2)−x)cosxsinx+xsinxcosx)/(cot^2 x+tan^2 x))dx 2I=∫_0 ^(π/2) (((π/2)sinxcosx)/(tan^2 x+cot^2 x))dx 2I=(π/2)∫_0 ^(π/2) ((tanxcos^2 x)/(tan^2 x+(1/(tan^2 x))))dx now I_1 =∫((tanx)/((1+tan^2 x)(tan^2 x+(1/(tan^2 x)))))dx t=tanx dt=sec^2 x dx (dt/(1+t^2 ))=dx ∫(t/((1+t^2 )(t^2 +(1/t^2 ))))×(dt/(1+t^2 )) ∫(t^3 /((1+t^2 )^2 (t^4 +1)))dt k=t^2 dk=2tdt (dk/2)=tdt ∫((k×(dk/2))/((1+k)^2 (1+k^2 ))) (1/4)∫((2kdk)/((1+k)^2 (1+k^2 ))) (1/4)∫(((1+k)^2 −(1+k^2 ))/((1+k)^2 (1+k^2 )))dk (1/4)∫(dk/(1+k^2 ))−(1/4)∫(dk/((1+k)^2 )) =(1/4)tan^(−1) (k)−(1/4)×(((1+k)^(−2+1) )/(−2+1)) =(1/4)tan^(−1) (k)+(1/(4(1+k))) =(1/4)tan^(−1) (t^2 )+(1/(4(1+t^2 ))) =(1/4)tan^(−1) (tan^2 x)+(1/(4(1+tan^2 x))) 2I=(π/2)×∣(1/4)tan^(−1) (tan^2 x)+(1/(4(1+tan^2 x)))∣_0 ^(π/2) 2I=(π/8)[{(tan^(−1) (tan^2 (π/2))+(1/(1+tan^2 (π/2))))}−{(tan^(−1) (0)+(1/(1+0)))}] I=(π/(16))[(tan^(−1) (∞)+(1/(1+∞)))−(1)] I=(π/(16))((π/2)+0−1) I=(π^2 /(32))−(π/(16)) pls check...](Q50545.png)
| ||
Question and Answers Forum | ||
Question Number 50414 by Abdo msup. last updated on 16/Dec/18 | ||
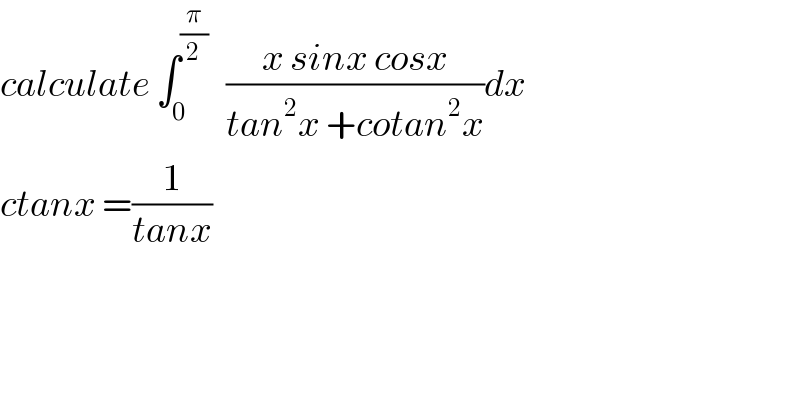 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Dec/18 | ||
![I=∫_0 ^(π/2) ((((π/2)−x)cosxsinx)/(cot^2 x+tan^2 x))dx 2I=∫_0 ^(π/2) ((((π/2)−x)cosxsinx+xsinxcosx)/(cot^2 x+tan^2 x))dx 2I=∫_0 ^(π/2) (((π/2)sinxcosx)/(tan^2 x+cot^2 x))dx 2I=(π/2)∫_0 ^(π/2) ((tanxcos^2 x)/(tan^2 x+(1/(tan^2 x))))dx now I_1 =∫((tanx)/((1+tan^2 x)(tan^2 x+(1/(tan^2 x)))))dx t=tanx dt=sec^2 x dx (dt/(1+t^2 ))=dx ∫(t/((1+t^2 )(t^2 +(1/t^2 ))))×(dt/(1+t^2 )) ∫(t^3 /((1+t^2 )^2 (t^4 +1)))dt k=t^2 dk=2tdt (dk/2)=tdt ∫((k×(dk/2))/((1+k)^2 (1+k^2 ))) (1/4)∫((2kdk)/((1+k)^2 (1+k^2 ))) (1/4)∫(((1+k)^2 −(1+k^2 ))/((1+k)^2 (1+k^2 )))dk (1/4)∫(dk/(1+k^2 ))−(1/4)∫(dk/((1+k)^2 )) =(1/4)tan^(−1) (k)−(1/4)×(((1+k)^(−2+1) )/(−2+1)) =(1/4)tan^(−1) (k)+(1/(4(1+k))) =(1/4)tan^(−1) (t^2 )+(1/(4(1+t^2 ))) =(1/4)tan^(−1) (tan^2 x)+(1/(4(1+tan^2 x))) 2I=(π/2)×∣(1/4)tan^(−1) (tan^2 x)+(1/(4(1+tan^2 x)))∣_0 ^(π/2) 2I=(π/8)[{(tan^(−1) (tan^2 (π/2))+(1/(1+tan^2 (π/2))))}−{(tan^(−1) (0)+(1/(1+0)))}] I=(π/(16))[(tan^(−1) (∞)+(1/(1+∞)))−(1)] I=(π/(16))((π/2)+0−1) I=(π^2 /(32))−(π/(16)) pls check...](Q50545.png) | ||
| ||